17.15 Описанная окружность и вписанный четырехугольник
Ошибка.
Попробуйте повторить позже
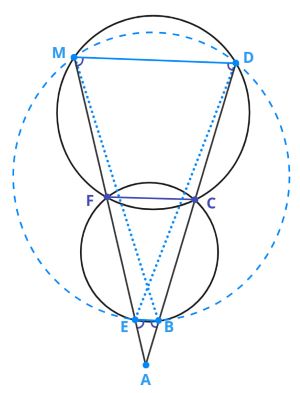
А вот и вторая геометрическая задачка из воспоминаний Деда Мороза: Две
окружности разных радиусов пересекаются в точках и
причем их
центры лежат по разные стороны от хорды
Вне обеих окружностей
взята точка
лежащая по ту же сторону от хорды
что и центр
меньшей окружности. Прямая
пересекает меньшую окружность в
точках
и
а большую — в точках
и
Прямая
пересекает
меньшую окружность в точках
и
а большую — в точках
и
а) Докажите, что =
б) Найдите сумму произведений длин противоположных сторон четырехугольника
если
и
а) Вспомним теорему о двух секущих и распишем ее для обеих окружностей.
Для меньшей окружности справедливо:
откуда
Для большей окружности справедливо:
откуда
Из двух пропорций, в которых левые части одинаковы, выводим:
Ч.Т.Д.
б)
1. В пункте а) мы доказали равенство:
Из него по обратной теореме Фалеса следует, что и
2. Из подобия выводим равенства углов:
3. В условии пункта б) утверждается, что С учетом с
прошлых двух тождеств этот тезис дает понять, что
и
на самом
деле равнобедренные.
4. Отсюда получаем, что трапеция также равнобедренная. У любой
равнобедренной трапеции сумма противоположных углов равна
следовательно, она вписанная.
5. Для вписанного четырехугольника справедлива теорема Птолемея, гласящая о том, что сумма произведений длин противоположных сторон вписанного четырехугольника равна произведению длин его диагоналей, то есть
NOTA BENE: Заметим, что теоремы Птолемея нет в учебниках федерального перечня, поэтому перед её применением на ЕГЭ следует привести её доказательство.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




