18.15 Функции. Область значений функций

Перепишем функцию в виде

Данная функция определена , так как ни при каком .

Сделаем замену , тогда новая функция

определена при . При этом области значений и совпадают.

1 способ

Так как функция непрерывна на всей области определения, то область значений функции содержит отрезок , если существуют такие точки и , что и . Следовательно, следующие уравнения должны иметь хотя бы по одному неотрицательному решению (т.к. функция определена для всех неотрицательных чисел):

При уравнение 1 не имеет решений, при уравнение 2 не имеет решений. Следовательно, эти значения параметра нам не подходят. При остальных уравнения 1 и 2 можно переписать в виде:

2 способ

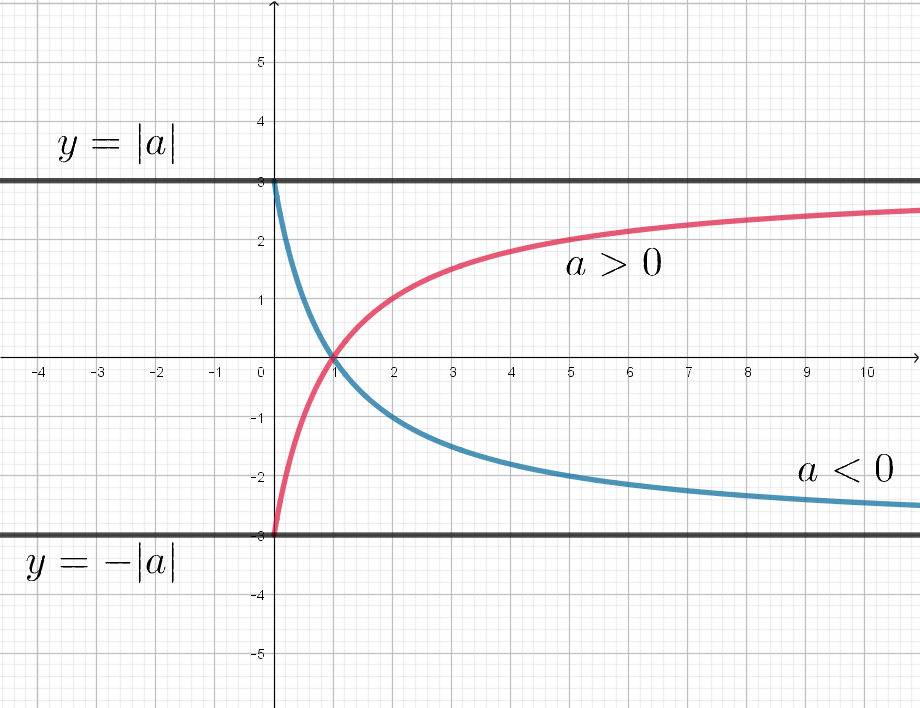
Графиком функции является часть ветви гиперболы при и константа при . Заметим, что при функция возрастает, а при убывает. Имеем:

График в зависимости от знака параметра выглядит следующим образом:

Таким образом, чтобы область значений функции содержала отрезок , нужно, чтобы

Случай мы не рассматриваем, так как функция, являющаяся константой, графически представляет собой горизонтальную прямую, следовательно, принимает только одно значение, то есть область ее значений не может содержать отрезок.