18.15 Функции. Область значений функций

Исследуем функцию через ее производную:

Дискриминант числителя равен

Следовательно, производная при любом имеет два нуля, причем заметим, что они разных знаков, так как их произведение равно . Назовем их и . Найдем знаки производной на промежутках, образованных этими нулями:

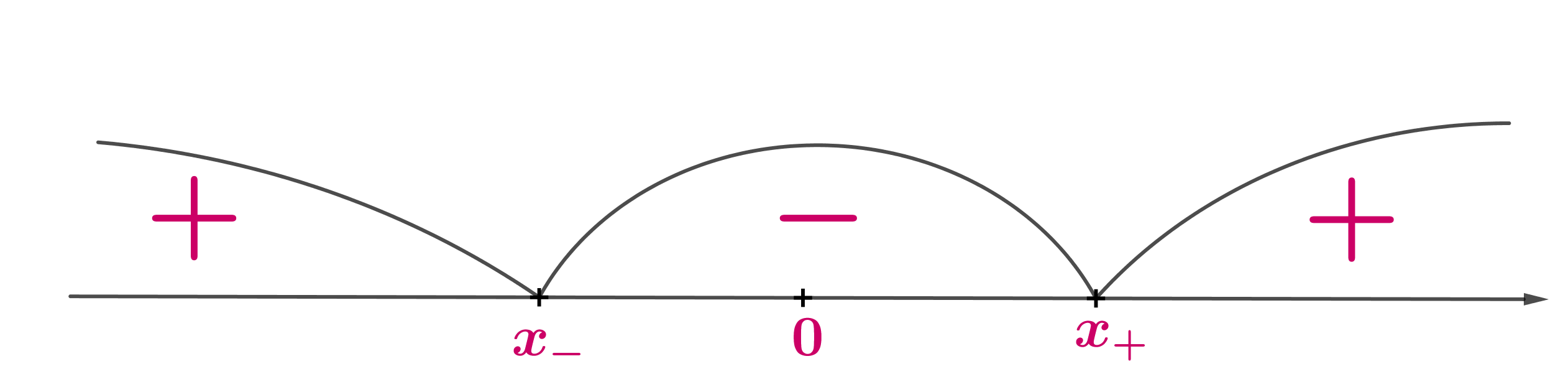
Заметим, что при имеем , следовательно, схематично график функции выглядит так:

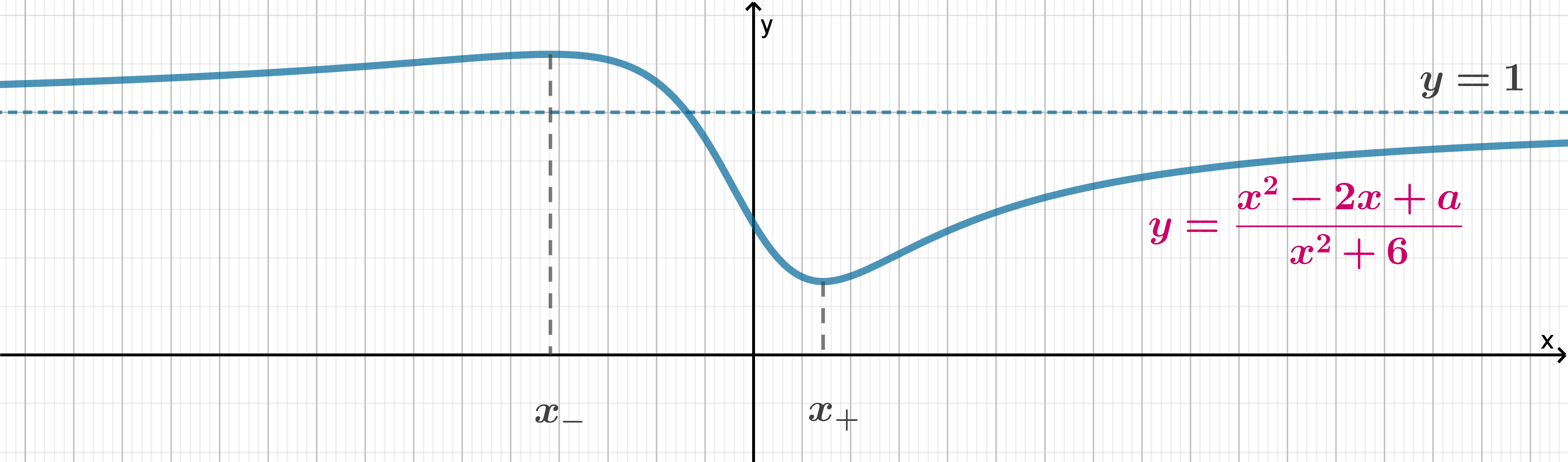
Таким образом, облласть значений функции и она точно содержит число . Следовательно, чтобы других целых чисел не было в области значений функции, нужно, чтобы и . Эти требования можно задать альтернативным условием: следующее неравенство должно быть выполнено для всех

Чтобы полученная система имела решения , каждое из неравенств должно иметь такие решения, следовательно, дискриминанты квадратичных трехчленов должны быть отрицательны одновременно: