18.15 Функции. Метод главного модуля/слагаемого
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых уравнение
имеет хотя бы одно решение.
Преобразуем левую часть уравнения:
Пусть Тогда графиком функции
является парабола с вершиной в точке
и ветвями,
направленными вниз. Это означает, что в точке
функция
принимает наибольшее из возможных значений, то есть
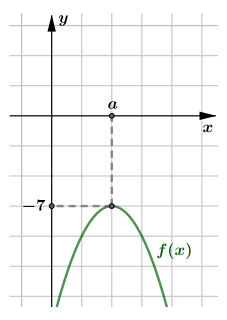
Рассмотрим правую часть уравнения. Пусть Воспользуемся принципом главного модуля, так как
только раскрытие первого модуля определяет, будет функция возрастать или убывать. Раскроем модули в функции
чтобы
убедиться в этом:
- Если
то при раскрытии первого модуля коэффициент при
будет равен
Заметим, что, как бы ни был раскрыт второй модуль, итоговый коэффициент при
будет отрицательным. Тогда на промежутке
функция
будет убывать.
- Если
то при раскрытии первого модуля коэффициент при
будет равен 6. Заметим, что, как бы ни был раскрыт второй модуль, итоговый коэффициент при
будет положительным. Тогда на промежутке
функция
будет возрастать.
Следовательно, в точке функция
будет принимать наименьшее из возможных значений, то есть
Нас просят найти такие значения параметра при которых исходное уравение будет иметь хотя бы одно решение. То есть
графики функций
и
должны иметь хотя бы одну точку пересечения. Заметим, что в точке
функция
принимает свое наибольшее значение, а функция
— наименьшее. Тогда если
то графики функций
и
вовсе не будут пересекаться.
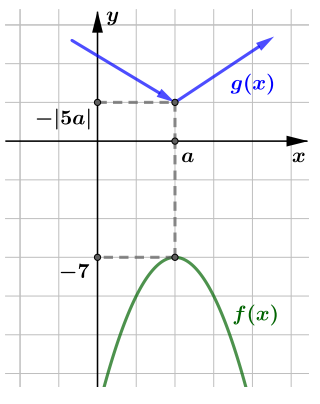
Следовательно, если у уравнения есть хотя бы один корень, то то есть
Заметим, что условия достаточно для того, чтобы исходное уравнение имело хотя бы одно решение, так как
принимает любое значение от
до
поэтому
примет значение, меньшее
а значит пересечет
график
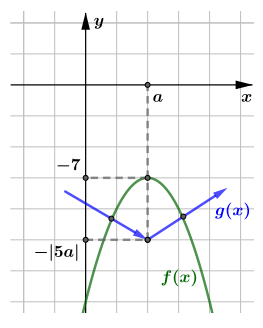
Следовательно, исходное уравнение имеет хотя бы одно решение при
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование либо в ходе рассмотрения функций, либо при решении неравенства | 3 |
| Обоснованный переход к неравенству, но его решение неверное | 2 |
| Введены и рассмотрены функции левой и правой части (аналитически или графически) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




