Перекладывание отрезков
Ошибка.
Попробуйте повторить позже
На плоскости отмечены две точки и
Андрей играет в такую игру: на каждом шаге он выбирает пару уже отмеченных точек,
мысленно строит правильный пятиугольник на них как на соседних вершинах, после чего отмечает на плоскости три остальные его
вершины. Сможет ли Андрей отметить середину отрезка
Источники:
Подсказка 1
Для начала подумаем, а как мы вообще можем изменять картинку? Например, можем ли мы повернуть отрезок, который уже у нас есть?
Подсказка 2
Да, мы можем повернуть отрезок на 108°, достроив на нём правильный пятиугольник! А как тогда повернуть отрезок на 180°?
Подсказка 3
Для этого мы можем совершить поворт на 108° пять раз! Получается, мы можем "перемещать" отрезок на прямой. Значит, чтобы получить точку внутри AB мы можем переместить какой-нибудь отрезок на прямой AB. Попробуйте для начала просто отметить какую-нибудь точку на этой прямой.
Подсказка 4
Постройте пятиугольник на AB, а потом на диагонали этого пятиугольника. Одна из вершин последней фигуры как раз будет лежать на AB. Осталось оценить длины отрезков и отложить некоторые из них так, чтобы получить точку внутри AB.
Вспомним, что угол правильного пятиугольника равен Поэтому, имея произвольный вектор
мы можем отложить равный ему по
длине вектор
так, чтобы
То есть, мы можем повернуть любой отрезок на
А проделав это 5 раз, мы повернём
отрезок на
Теперь предложим алгоритм решения задачи. По точкам и
отметим вершины пятиугольника
а потом пятиугольника
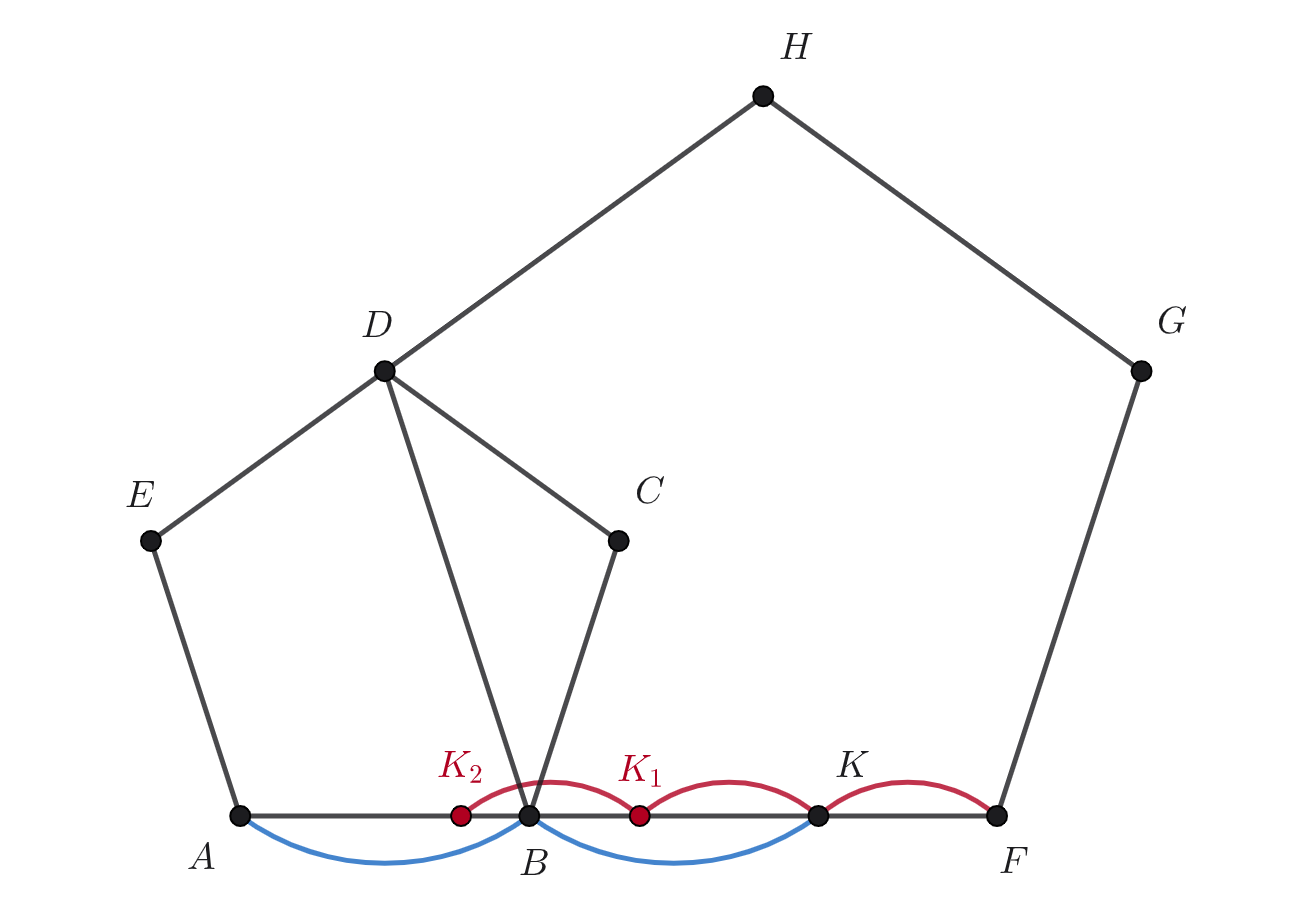
Заметим, что — диагональ
поэтому
То есть сторона пятиугольника
больше стороны
пятиугольника
но меньше, чем удвоенная сторона этого же пятиугольника. Отсюда,
Так же заметим, что
Тогда откуда
То есть точки
лежат на одной
прямой.
Повернём вектор на
и получим Вектор
При этом
принадлежит
а так же
так как
Поэтому, если несколько раз отложить
то есть сначала повернуть
на
и получить
затем так же повернуть
и получить
и так далее, то какая-то из точек
окажется на отрезке
Нет
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




