Лемма 255
Ошибка.
Попробуйте повторить позже
Окружность с центром вписана в треугольник
и касается его сторон
,
и
в точках
и
соответственно.
Прямые
и
пересекают прямую
в точках
и
Докажите, что центр окружности, описанной около треугольника
, точка
и точка
лежат на одной прямой.
Источники:
Подсказка 1
Учтите ловушку задачи, что точка О это центр вписанной окружности, а не описанной! На пересечении каких объектов лежит центр вписанной (!) окружности?
Подсказка 2
Конечно! Тогда для работы с биссектрисами углы треугольника удобнее обозначать за 2альфа, 2бетта, 2 гамма. Теперь надо понять: на пересечении каких объектов лежит центр описанной (!) окружности?
Подсказка 3
Давайте отметим точку Т пересечения DO и серединного перпендикуляра к стороне ON. Наша цель - показать, что эта точка T является пересечением всех серединных перпендикуляров, то есть центром описанной окружности. Как можно подступиться к центру окружности в терминах углов?
Подсказка 4
Через центральный и вписанный угол! Нужно доказать, что угол OTN в два раза больше фиксированного угла OMN. Осталось досчитать углы!
Первое решение.
![]()
Обозначим углы через
. Тогда
и
Здесь и выбрана из условия
Заметим, что такое расположение точки обусловлено тем, что
. Далее
из
равенства отрезков касательных. Тогда
То есть , а также эта точка лежит на серединном перпендикуляре к
в силу выбора
. Тогда
она должна являться центром описанной окружности
, поскольку для неё это свойство выполнено, а для точек
“выше” и “ниже” на прямой
будет меньше и больше соответственно (то есть точка, из которой видна
под
углом
всего одна). Здесь важно заметить, что центр описанной окружности лежит именно по эту сторону от
,
поскольку
______________________________________________________________________________________________________________________________________________________
Второе решение. Продолжим отрезки и
до пересечения в точке
.
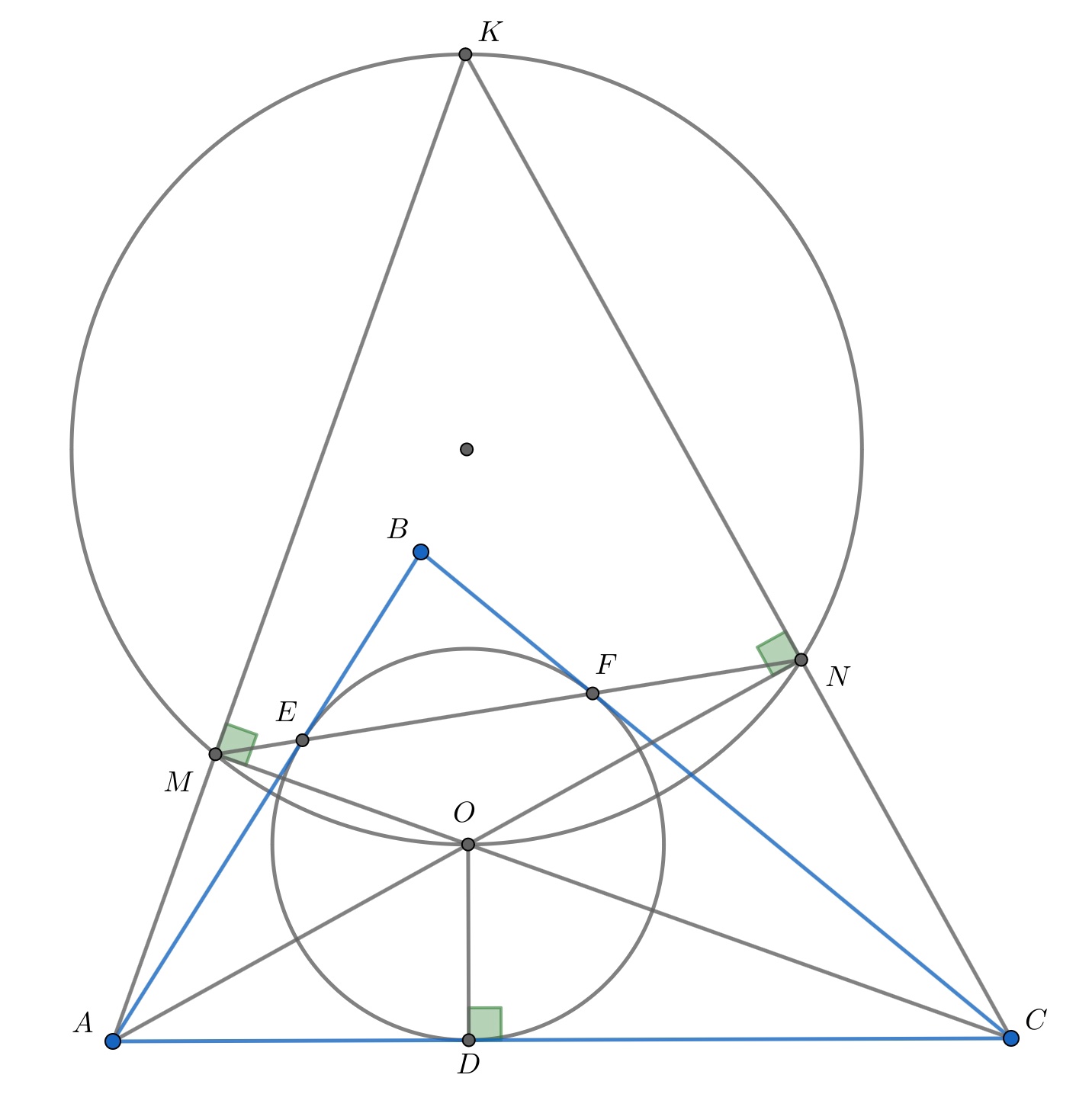
Из леммы получаем, что
и
— высоты треугольника
, а
— его ортоцентр. Поскольку
, то точка
—
основание третьей высоты треугольника
. Точки
и
лежат на окружности с диаметром
поэтому центр этой окружности,
как и точка
лежит на прямой
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




