Лемма 255
Ошибка.
Попробуйте повторить позже
Дан треугольник 
На продолжении стороны 
за точку 
отмечена точка 
Окружности, вписанные в треугольники 
и
пересекаются в точках 
и 
Докажите, что все прямые 
проходят через одну и ту же точку, не зависящую от выбора точки
Пусть окружности, вписанные в треугольники 
и 
касаются прямых 
и 
в точках 
Пусть биссектриса угла
пересекает прямую 
в точке 
По лемме 
точка 
является проекцией точки 
на эту биссектрису, и поэтому 
не
зависит от выбора точки 
Аналогично, прямая 
проходит через фиксированную точку 
— проекцию точки 
на биссектрису
угла 
Прямые 
и 
параллельны, так как они перпендикулярны биссектрисе угла 
Пусть прямая 
пересекает
прямые 
и 
в точках 
и 
соответственно.
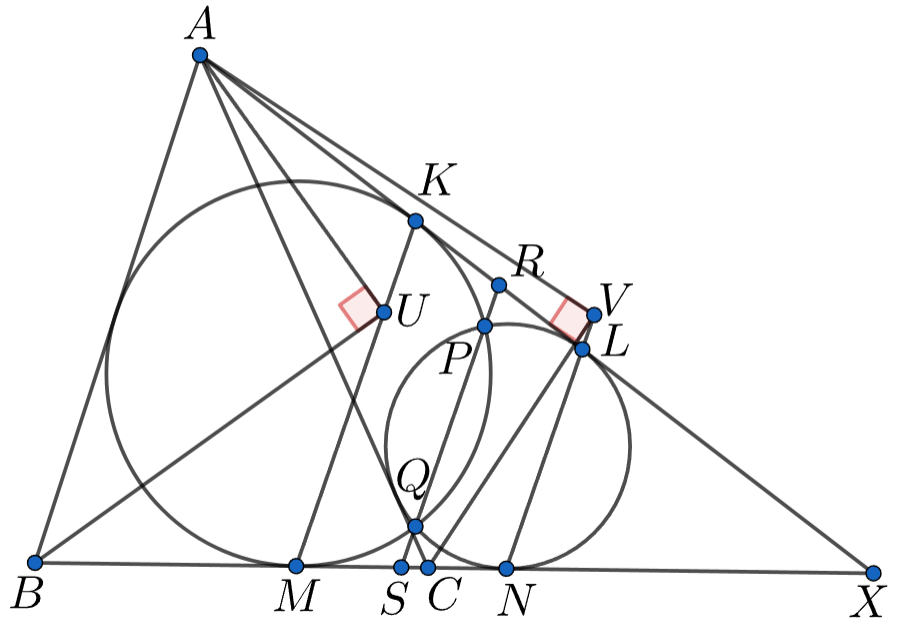
По теореме о касательной и секущей, 
то есть 
Аналогично, 
Таким образом, прямая 
является средней линией трапеции 
Значит, прямая 
делит пополам любой отрезок, соединяющий точки на прямых 
и
в частности, проходит через фиксированную точку — середину отрезка 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
