Прямая Симсона

Пусть прямые, симметричные пересекаются в точке Тогда точки, симметричные лежат на а, значит, проекции на стороны треугольника лежат на одной прямой (потому что гомотетия с центром в и коэффициентом переводит точки, симметричные в проекции на стороны треугольника). Отсюда, по теореме Симсона, точка лежит на описанной окружности Докажем теперь следующую лемму.

_________________________________________________________________________________________________________________________________________________________________________________

Лемма. Если высоты треугольника пересекаются в точке а — точка его описанной окружности, то прямая Симсона точки относительно треугольника делит отрезок пополам.

Доказательство. Пусть не умаляя общности точка находится на меньшой дуге Проведем хорду перпендикулярную Пусть точки и симметричны точкам и относительно прямой точка лежит на описанной окружности треугольника

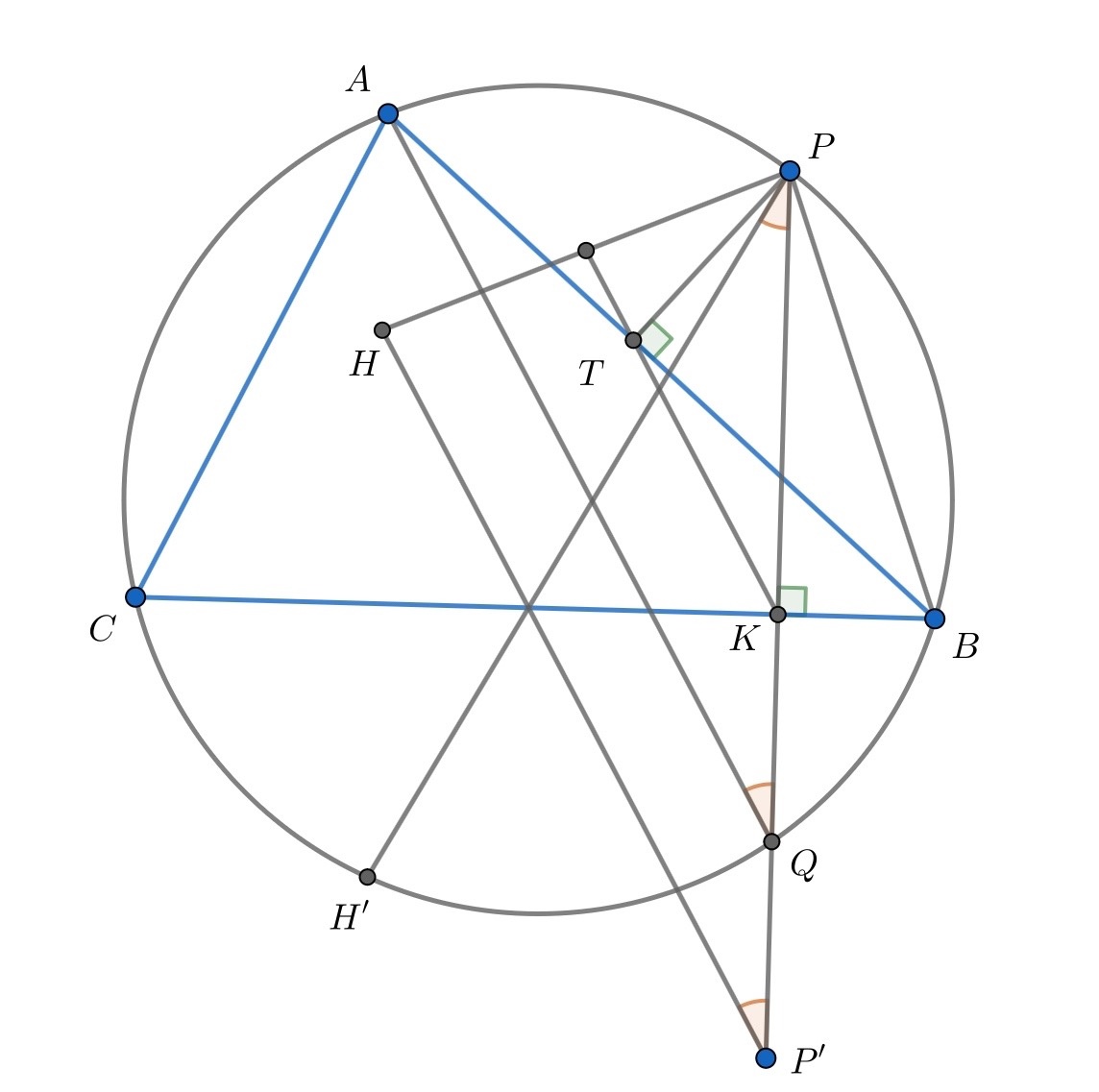
Докажем сначала, что В самом деле, Теперь докажем, что параллельна прямой Симсона. Пусть пересекает в точке Так же опустим перпендикуляр на Тогда у нас вписанный. В таком случае есть две пары антипараллельных прямых относительно и Это будут и и Отсюда следует, что и параллельны, где и есть прямая Симсона. Значит, она проходит через середину стороны треугольника и параллельна стороне а, значит, она проходит через середину стороны

Пусть не умаляя общности точка находится на меньшой дуге Тогда пересекает в точке Так же опустим перпендикуляр на Тогда у нас вписанный. В таком случае есть две пары антипараллельных прямых относительно и Это будут и и Отсюда следует, что и параллельны, где и есть прямая Симсона.

_________________________________________________________________________________________________________________________________________________________________________________

Из леммы получаем, что прямая Симсона проходит через середину отрезка Как уже было отмечено, гомотетия с центром в и коэффициентом переводит прямую Симсона точки в прямую а середину отрезка  – в точку Получается, прямая содержит точку Так как определение точки не зависит от выбора прямой мы получили, что все прямые, описанные в задаче, проходят через одну и ту же точку