Расположение точек, отрезков и прямых
Ошибка.
Попробуйте повторить позже
Через три стороны правильного 30-угольника проводят прямые. Стороны выбирают так, что прямые пересекаются друг с другом, и исходный многоугольник лежит внутри полученного треугольника.
Сколько попарно неравных треугольников может получиться? Равными считаются треугольники, которые можно совместить поворотом или отражением.
Источники:
Подсказка 1
Пусть чётное n — число сторон многоугольника. Сколько есть способов выбрать тройку его сторон (a,b,c)?
Подсказка 2
n⋅(n-1)⋅(n-2). Но ведь не любые 3 стороны образуют треугольник, к тому же, разные тройки могут порождать одинаковые по форме фигуры. Какие фигуры нам надо различать для правильного подсчёта?
Подсказка 3
Нам понадобится различать равносторонние, равнобедренные и прочие треугольники, так как у них разное количество симметрий. Давайте считать, что (a,b,c) расположены против часовой стрелки. Попробуйте посчитать количество треугольников.
Подсказка 4
a можно выбрать n способами, теперь пометим параллельную a сторону красным. Сколько есть вариантов для выбора b?
Подсказка 5
Для выбора b отсчитываем k сторон от a, где k = {0;1;2;...;(n-2)/2 - 1}. Пометим параллельную b сторону синим. Сколько есть вариантов для выбора c?
Подсказка 6
Для выбора c останутся только стороны между красной и синей — получится ровно k вариантов. Сколько всего треугольников получится? Не забудьте учесть случаи, когда (a,b,c) расположены по часовой стрелке.
Подсказка 7
Получится n ⋅ (0 + 1 + 2 + ... + (n-2)/2 - 1) ⋅ 2/6 с учетом расположения по часовой стрелке и исключением перестановок. Преобразуйте выражение.
Подсказка 8
S = n⋅(n-2)⋅(n-4)/24. Теперь посчитайте количество равнобедренных (но не равносторонних) треугольников.
Подсказка 9
Выберем основание n способами. Под каким углом к основанию можно выбрать правую боковую сторону?
Подсказка 10
Она должна пересекаться с основанием под острым углом (но не 60°). Что можно сказать про левую боковую сторону?
Подсказка 11
она будет достроена однозначно. Сколько есть вариантов выбрать правую боковую сторону?
Подсказка 12
Есть (n-4)/4 вариантов, если n делится на 4, и (n-2)/2 - в ином случае. Также нужно учесть случай, когда угол равен 60°. При каком n будет такая боковая сторона?
Подсказка 13
Такая сторона будет, если n кратно 3. Теперь разберите все возможные случаи для равнобедренных (но не равносторонних) треугольников.
Подсказка 14
Когда можно выбрать равносторонний треугольник?
Подсказка 15
Из рассуждений о равнобедренных треугольниках, когда n кратно 3. Разберите случаи.
Подсказка 16
Сколько будет неравнобедренных треугольников?
Подсказка 17
Из общего количества треугольников нужно вычесть количества равнобедренных и равносторонних. Теперь учтите повороты и отражения для каждого типа.
Пусть — число сторон многоугольника. Пусть
чётное. Всего способов выбрать тройку сторон
из имеющихся
будет
Правда, не каждая тройка порождает треугольник, и разные тройки могут порождать одинаковые по форме фигуры. Для
правильного подсчёта нам понадобится различать равносторонние, равнобедренные и остальные треугольники, так как у них разное
количество симметрий.
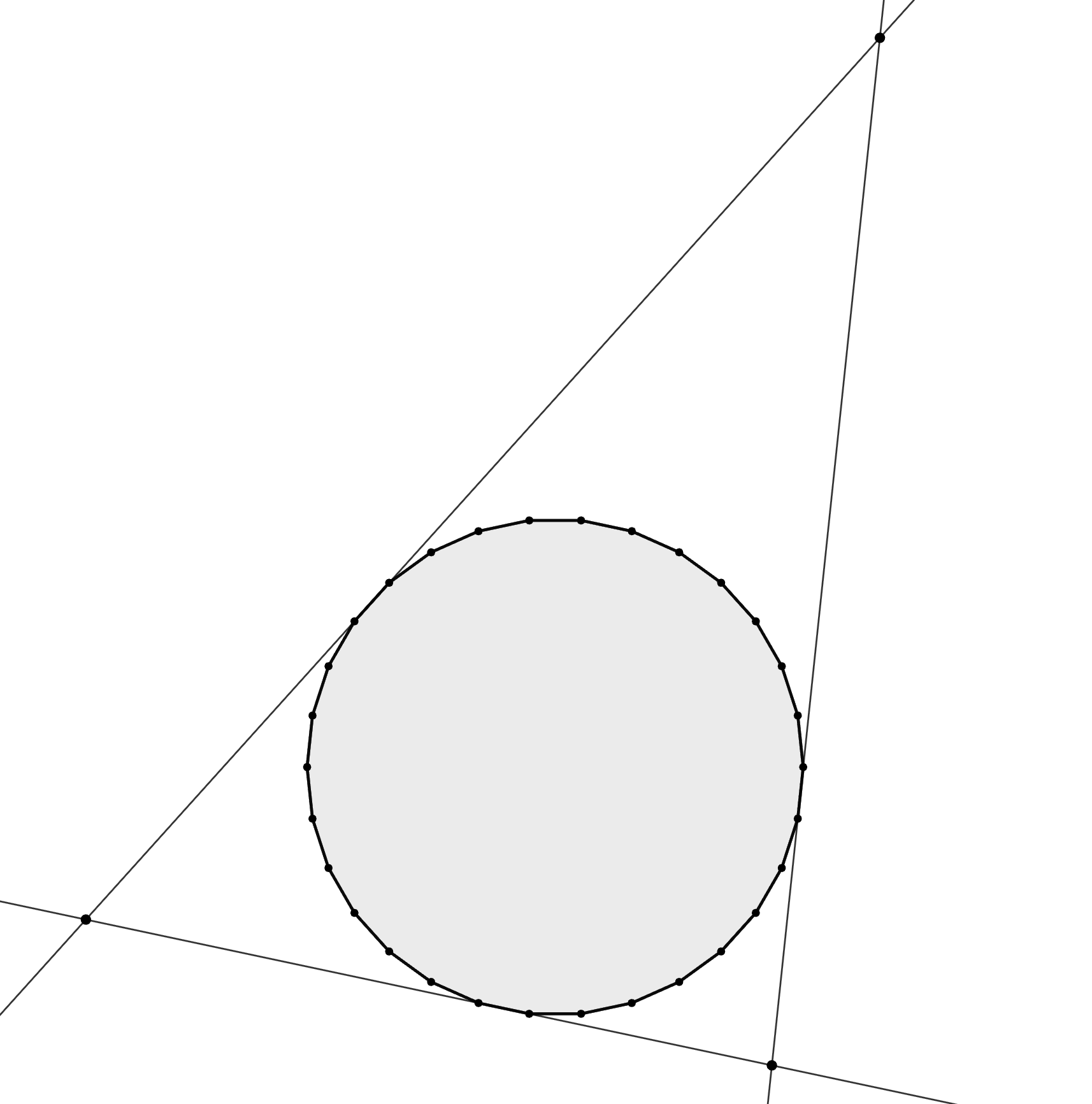
Давайте считать, что расположены против часовой стрелки. Первую сторону треугольника
можно выбрать
способами.
Пометим параллельную
сторону красным. Для выбора второй стороны
отсчитываем
сторон от
где
Помечаем параллельную
сторону синим. Для выбора c остаются только стороны между красной и синей сторонами –— и вариантов
выбора будет ровно
Значит, всего треугольников будет
(умножаем на
чтобы учесть тройки, где
расположены по часовой, и делим на
для учёта всех перестановок
между собой). Используем формулу суммы прогрессии,
получаем, что всего треугольников будет
Посчитаем, сколько будет равнобедренных (но не равносторонних) треугольников. Основание можно выбрать способами, правую
боковую сторону выбираем так, чтобы она пересекалась с основанием под острым углом (но не
Левая боковая сторона будет
достроена однозначно. Для выбора боковой стороны есть
вариантов (если
делится на
и
в ином случае, и ещё нужно
отнять одну сторону под углом
которая будет, если
делится на
Равнобедренных треугольников будет (
—
целые)
- 1.
-
если
- 2.
-
если
- 3.
-
если
- 4.
-
если
Равносторонний треугольник можно выбрать, если делится на
Таких треугольников будет
штук. Если
на
не делится, то
их не будет.
- 1.
-
если
- 2.
-
если
Значит, у нас есть неравнобедренных,
равнобедренных неравносторонних и
равносторонних
треугольников.
Теперь учтём повороты и отражения. Равносторонний треугольник на самом деле единственный. Каждый равнобедренный (но не
равносторонний) треугольник имеет равных себе, полученных поворотами. Неравнобедренный треугольник можно поворачивать
способами и отражать, что даёт
равных ему.
Значит, ответ (в общем случае при чётном ) равен:
А при ответ равен
19
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




