Расположение точек, отрезков и прямых
Ошибка.
Попробуйте повторить позже
С выпуклым четырехугольником проделывают следующую операцию: одну из данных вершин меняют на точку, симметричную
этой вершине относительно серединного перпендикуляра к диагонали (концом которой она не является), обозначив новую точку прежней
буквой. Эту операцию последовательно применяют к вершинам
— всего
раз. Назовем четырехугольник
допустимым, если его стороны попарно различны и после применения любого числа операций он остается выпуклым. Существует
ли
(a) допустимый четырехугольник, который после операций становится равным исходному?
(b) такое число что любой допустимый четырехугольник после
операций становится равным исходному?
Подсказка 1
Есть ли точки в четырёхугольнике, положение которых остаётся неизменным при выполнении операций?
Подсказка 2
Рассмотрим точку O — пересечение серединных перпендикуляров к диагоналям. Остаётся ли положение этой точки неизменным при выполнении операций?
Подсказка 3
Разделим четырёхугольник на треугольники △AOB, △BOC, △COD, △DOA. При операции над вершиной A (симметрия относительно перпендикуляра к BD) сравните △A'OD и △AOB, где A' — точка, в которую перейдёт A. Что можно сказать об их сторонах и углах? Сколько операций потребуется, чтобы △A'OD поменял свой вид?
Подсказка 4
После замены A на A' получаем △A'OD ≅ △AOB. Как это преобразование влияет на соседние треугольники?
Подсказка 5
По своей сути операция отражает или переворачивает треугольники.
Подсказка 6
Последовательно примените операции к A, B, C. Как теперь выглядит конфигурация треугольников вокруг O? Какие стороны имеет новый четырёхугольник A'B'C'D? В каком порядке идут его стороны?
Подсказка 7
Предположим, исходный четырёхугольник вписан в окружность. Как связана точка O с окружностью? Сохраняются ли длины сторон после трёх операций? Что определяет форму вписанного четырёхугольника при фиксированной окружности?
Подсказка 8
Можем ли мы построить вписанный четырёхугольник с попарно различными сторонами? Будет ли он возвращаться в себя после трёх операций?
Если — вписанный четырёхугольник, то он перейдёт в равный четырёхугольник за три операции. Любой допустимый
четырёхугольник перейдёт в равный ему четырёхугольник за
операций,
(например, за
Обозначим через точку пересечения серединных перпендикуляров к диагоналям. Заметим, что эта точка остаётся на месте при
применении любого количества операций к четырёхугольнику. Обозначим через
…,
углы, образованные сторонами
четырёхугольника и отрезками
(см. рис. ниже).
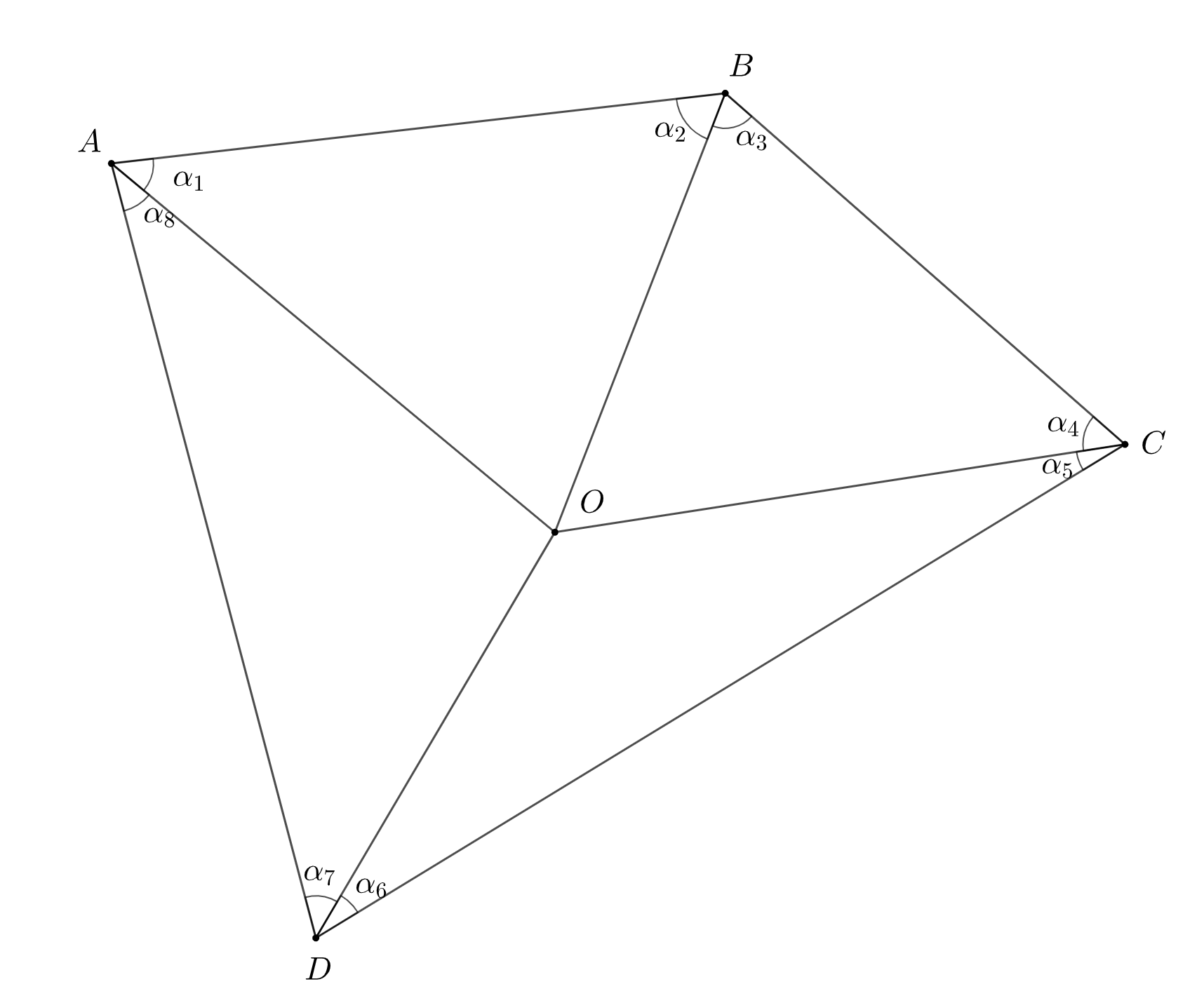
После применения одной операции обозначим образ точки как
Тогда
в силу симметрии, то есть
операция отражает треугольники, образованные стороной четырёхугольника и соответствующей парой отрезков к точке
Обозначим образы точек
и
после соответствующих операций как
и
соответственно. Тогда аналогично
Таким образом,
(равенство углов отмечено на рис.
ниже).
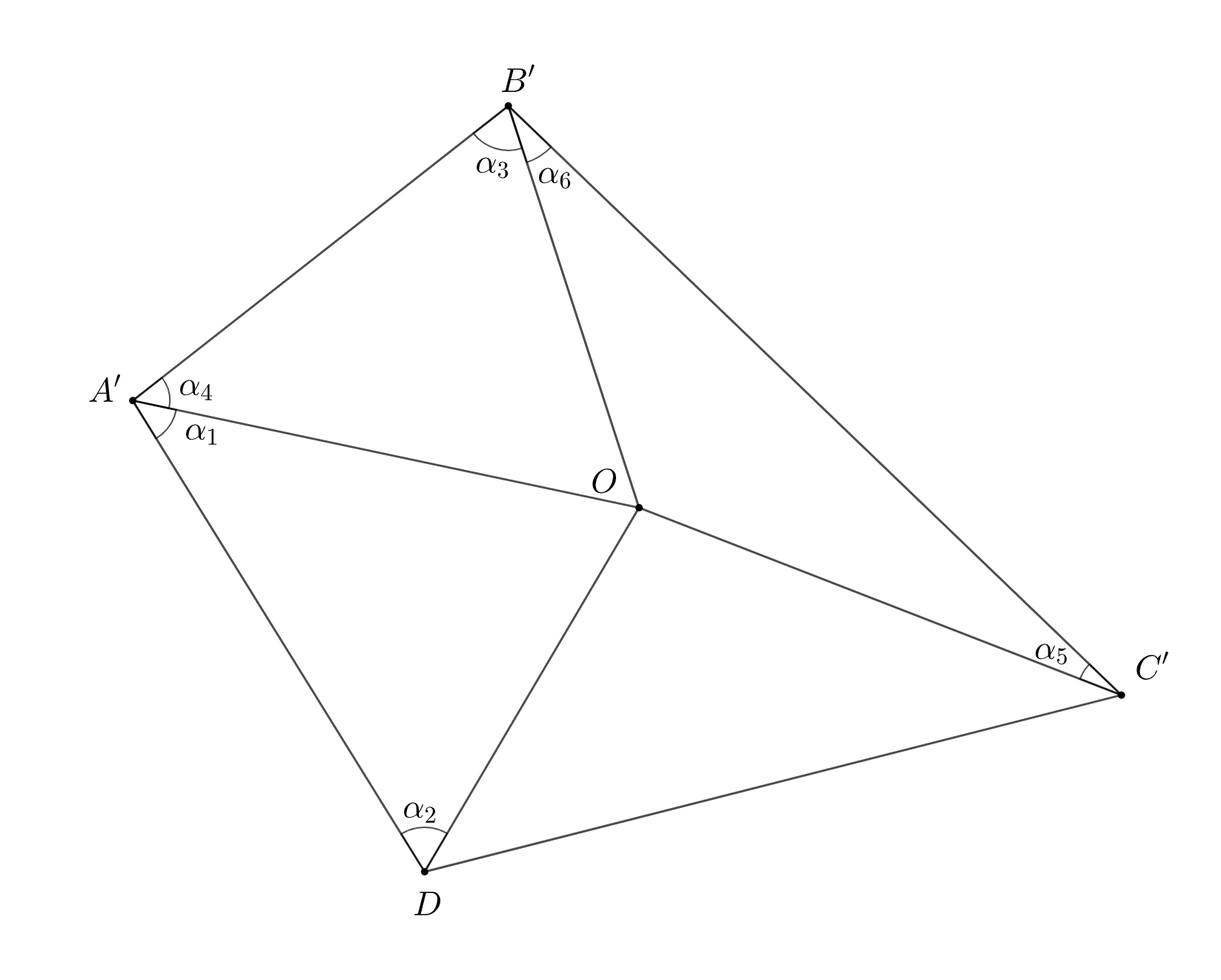
Тогда
следовательно, Значит, после применения трёх операций стороны четырёхугольника опять будут стоять в прежнем
порядке, а указанные углы будут расположены, как указано на рисунке ниже.
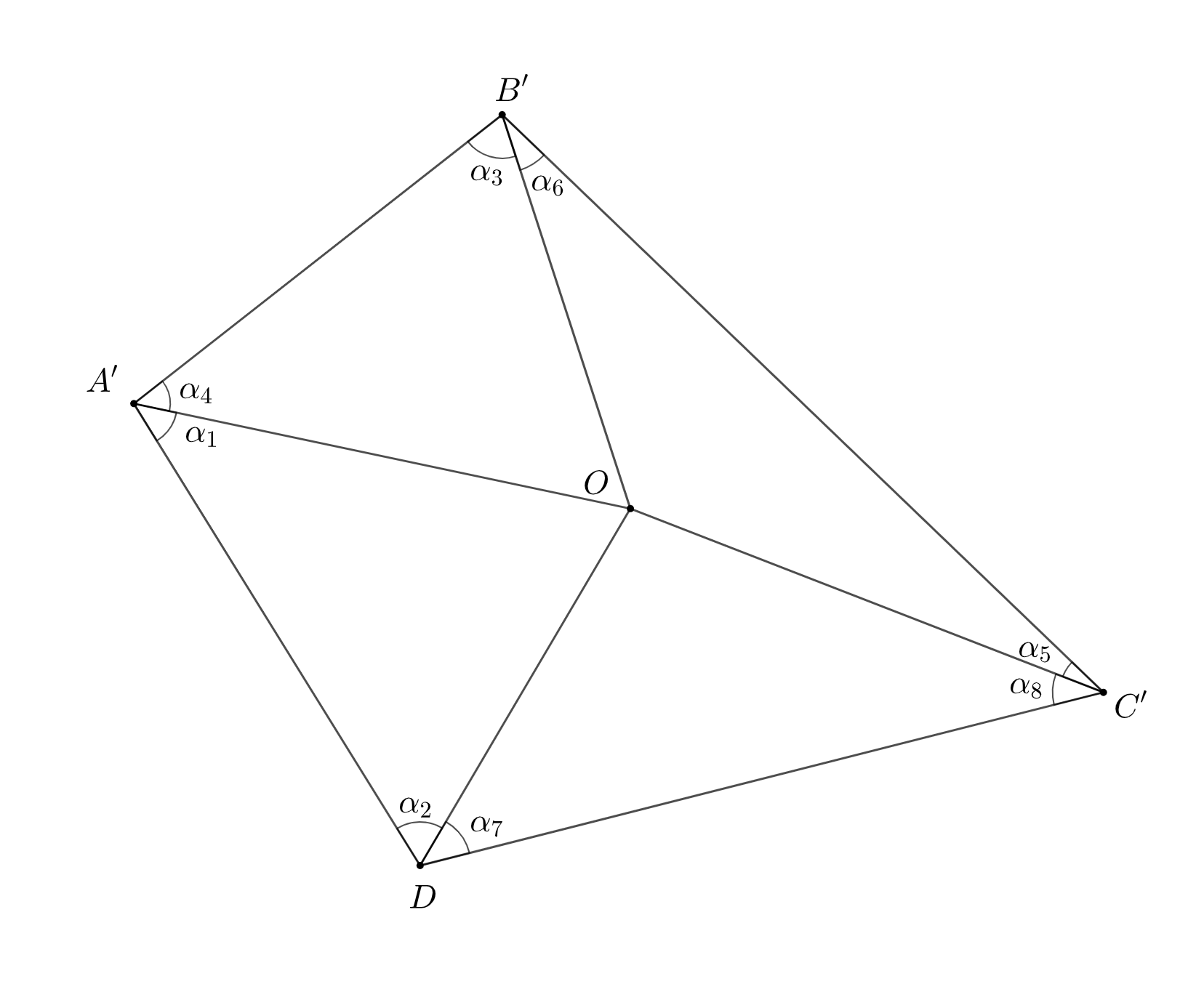
Если — вписанный четырёхугольник, то
— центр описанной окружности, и такой четырёхугольник полностью задаётся
длинами сторон, их порядком и описанной окружностью. Четырёхугольник, получающийся через три операции, также вписан в ту же
окружность, так как
и имеет те же стороны, что и исходный, следовательно, равен ему.
После шести операций стороны опять будут расположены в прежнем порядке, и углы будут расположены так же, как в исходном
четырёхугольнике, так как операция отражает треугольники, образованные стороной четырёхугольника и соответствующей парой отрезков
к точке
(a) и (b) да, существует.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




