Расположение точек, отрезков и прямых
Ошибка.
Попробуйте повторить позже
С четырехугольником проделывают следующую операцию: одну из данных вершин меняют на точку, симметричную этой вершине
относительно середины диагонали (концом которой она не является), обозначив новую точку прежней буквой. Эту операцию
последовательно применяют к вершинам
…. Докажите, что в некоторые два разных момента времени получатся два
равных четырехугольника.
Введем систему координат с центром в произвольной точке Сопоставим вершинам квадрата
векторы
Посмотрим как меняются данные векторы при данных операциях.
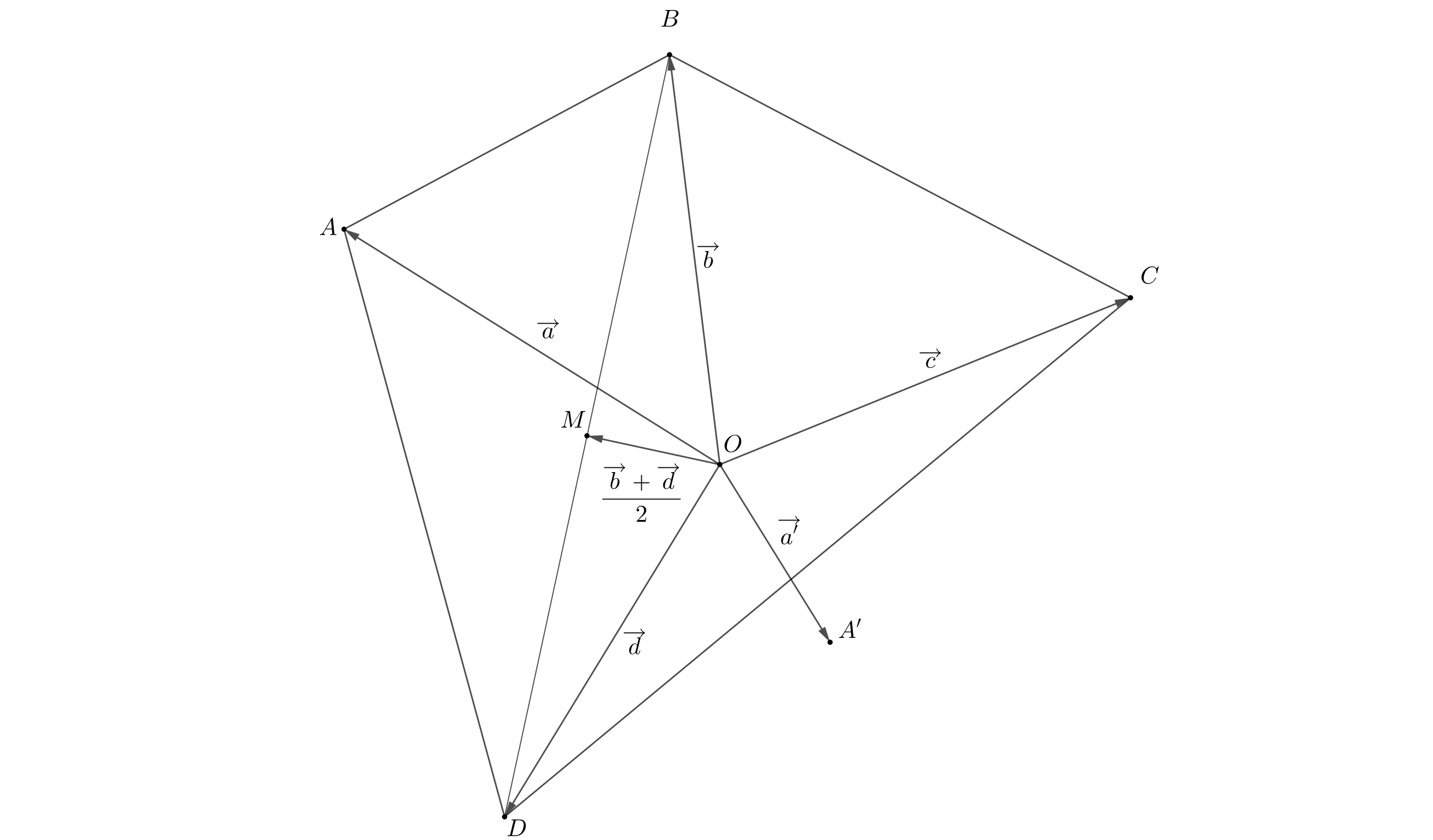
Пусть точка перешла в
тогда
— середина
является серединой
то есть
Трижды проведем данные операции и посмотрим на соответствующие вершинам векторы:
Четырехугольник определяется векторами сторон и порядком обхода, для исходного данные вектора равны:
а для четырехугольника полученного через три операции:
то есть отличаются только циклическим сдвигом, значит, данные четырехугольники равны.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




