Расположение точек, отрезков и прямых

Рассмотрим одну точку. По условию, ее можно соединить плохим отрезком с некоторой второй точкой, а на отрезке будет лежать третья. Третью точку тоже нужно соединить плохим отрезком с какой-нибудь точкой, но при этом нельзя с первой или второй, так как тогда будет уже точки на одной прямой. Значит, третья соединяется с четвертой, а на отрезке будет лежать пятая. Заметим, что при этом пятая точка не может быть соединена плохим отрезком ни с какой из первых четырех. Значит, нужно использовать еще хотя бы одну точку, т. е. 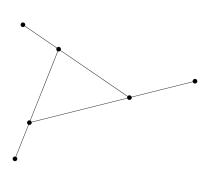точек не меньше 6. Пример приведён на рисунке.