Конструктивы в комбигео

При очевидно: все точки одного цвета. Пусть будем доказывать от противного. Заметим, что среди любых точек найдутся две одноцветные (для определенности будем говорить, что они красного цвета). Рассмотрим две одноцветные точки, лежащие на одной горизонтальной прямой, и треугольник, образованный ими. Тогда третья вершина будет не красной, пусть синей. В любом квадрате размера найдётся равнобедренный треугольник, у которого вершины на горизонтальном катете одноцветны, а третья — другого цвета.

Теперь рассмотрим квадрат Точки внутри него индуцируют раскраску квадрата, и всего таких раскрасок Рассмотрим квадратов, лежащих на одной горизонтальной прямой (т.е. при горизонтальных сдвигах переходящих друг в друга). Найдутся два квадрата с одинаковой раскраской, тогда у них внутри найдутся два одинаковых треугольника. Посмотрим на узел в пересечении прямых гипотенузы первого и вертикального катета второго (см. рисунок).

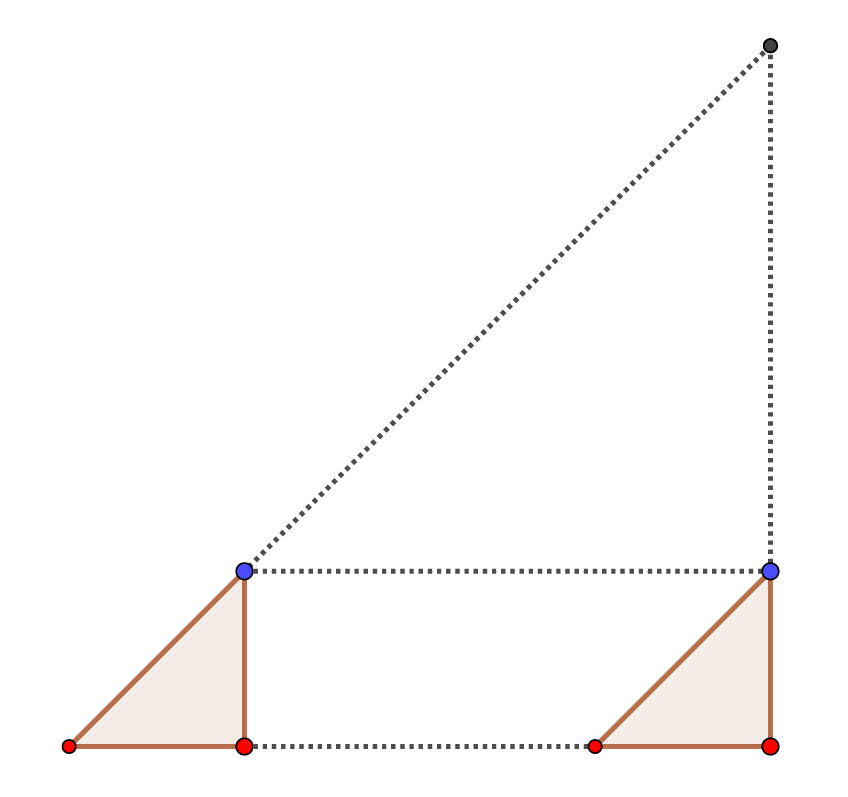
Вершина, отмеченная серым цветом на рисунке, не может быть синего или красного цвета. При мы бы уже получили противоречие. Заметим, что построенная конструкция находится в квадрате и в любом квадрате такого размера такая конструкция найдется. Повторим построение: рассмотрим квадратов размера Снова найдутся два с одинаковой раскраской и одинаковыми конструкциями внутри. Посмотрим на аналогичную точку пересечения: у неё теперь три запрета на возможные цвета. Размер стороны квадрата, в котором это содержится, обозначим В любом квадрате со стороной найдется конструкция, у верхней вершины которой (серой на рисунках для случаев двух и трёх цветов) будет запрета на цвет.

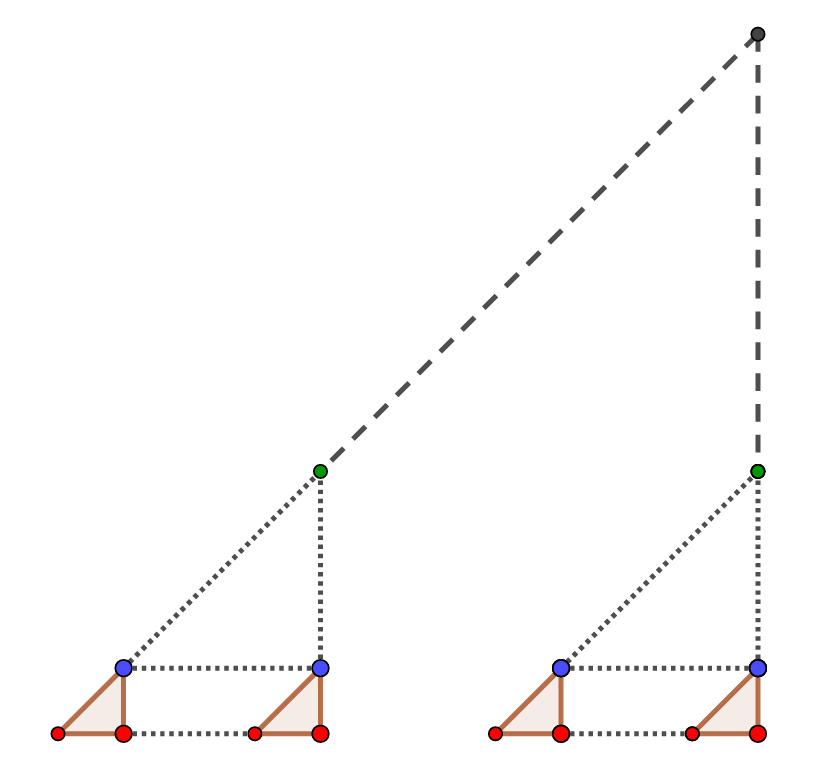
Обобщим рассуждения. Пусть — размер квадрата, в котором найдется индуктивно построенная конструкция, причём у верхней вершины будет запретов на цвет (так как есть пар точек, лежащих на одной горизонтальной прямой, причём одна из них лежит на гипотенузе, а другая — на вертикальном катете). Повторяя рассуждения для меньших случаев, в квадрате размера будет лежать конструкция с запретом на цвет верхней вершины. Тогда в квадрате со стороной все цвета будут запрещены, что приводит к противоречию.