Конструктивы в комбигео

Ключевое наблюдение: треугольник остроугольный тогда и только тогда, когда центр описанной окружности лежит внутри него. Рассмотрим произвольные четыре точки на окружности. В любом четырёхугольнике, вписанном в окружность, хотя бы два из четырёх треугольников будут тупоугольными. Действительно, если все четыре точки лежат на одной полуокружности, то все четыре треугольника тупоугольные. В противном случае, разбивая четырёхугольник диагональю, получим два треугольника, содержащих центр (острые) и два не содержащих (тупые).

Умножая количество четырёхугольников на получаем нижнюю оценку общего числа тупоугольных треугольников:

Каждый тупоугольный треугольник попадает ровно в четырёхугольник. Следовательно, истинное количество тупоугольных треугольников хотя бы:

Сравнивая с общим числом треугольников получаем, что доля тупоугольных не менее половины. Равенство возможно только, если в каждом четырёхугольнике ровно два тупоугольных треугольника, что достигается при

Если четыре точки лежат на одной полуокружности, то любой треугольник из трёх таких точек будет содержаться в полуокружности, а значит, центр окружности не попадёт внутрь. Следовательно, все таких треугольника будут тупоугольными. Для по принципу Дирихле обязательно найдётся четвёрка точек на одной полуокружности, что нарушит условие равенства половины.

• треугольников нет.
• треугольник один.
• пример на рисунке:
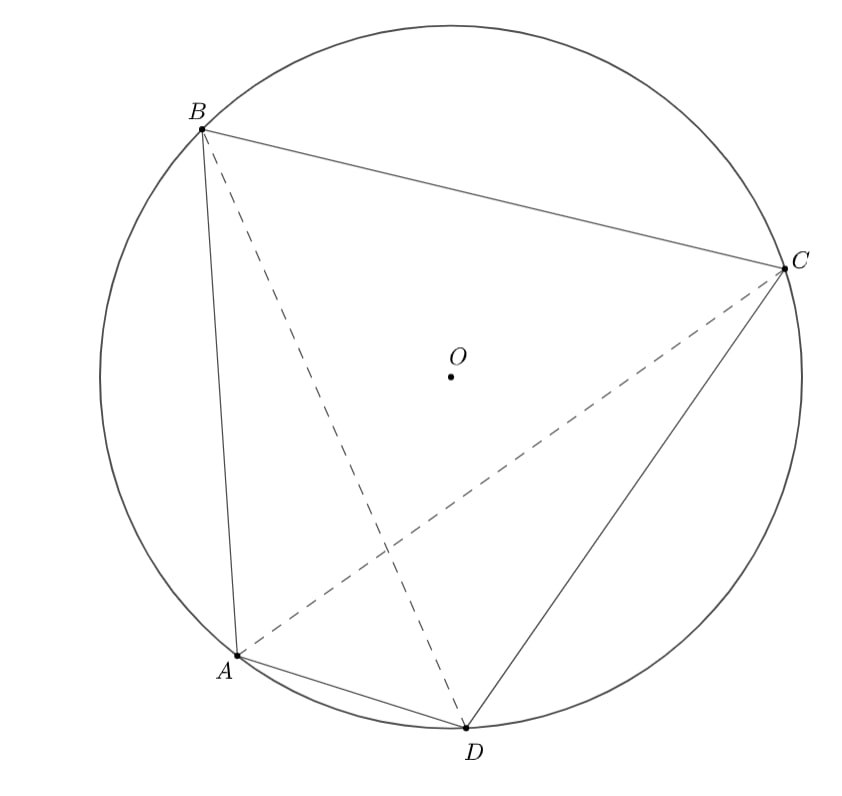
• подходит правильный пятиугольник.