Конструктивы в комбигео

Докажем, сначала, что для раскраски целочисленных точек в цветов любом квадрате достаточно большого размер, имеющего целые вершины и границы, параллельные линиям сетки, найдется одноцветный равнобедренный треугольник у которого и являются катетами, а также вершина находится ниже вершины и правее вершины Доказывать это утверждение будем индукцией по База для очевидна. Будем обозначать сторону квадрата из утверждения через Тогда берем Выберем произвольную горизонтальную прямую. Тогда по теореме ван дер Вардена для отрезка длины найдется одноцветная арифметическая прогрессия длины . Обозначим координаты этих точек через (не нарушая общности, можно считать координаты такими), и пусть они все покрашены в первый цвет. Рассмотрим решетку со стороной содержащую точку Тогда заметим, что точки этой решетки, принадлежащие треугольнику с координатами не могут быть покрашены в первый цвет (иначе требуемый прямоугольный треугольник уже был бы найден). С другой стороны внутрь выделенного треугольника помещается квадрат со стороной Тогда требуемый прямоугольный треугольник найдется по предположению индукции в данном квадрате (с новой решеткой). В качестве нам подойдет

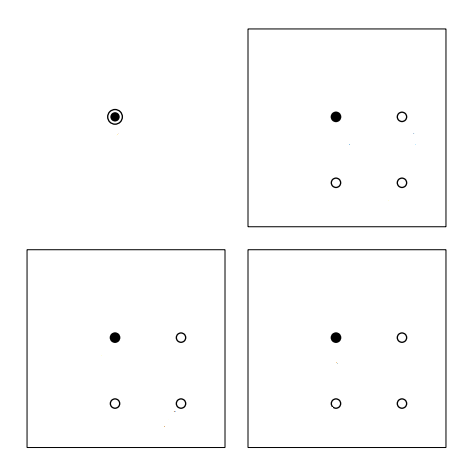
Перейдем к решению задачи. Разобьем все целые точки на квадраты со стороной Будем каждый квадрат считать точкой. Цвет квадрата определим как набор цветов его целочисленный точек (то есть всего цветов не больше ). Тогда по ранее доказанному найдется равнобедренный прямоугольный треугольник с вершинами — квадратами. Но в каждом таком квадрате есть равнобедренный прямоугольный треугольник. Тогда имеем конструкцию как на рисунке. Будем считать, что наши цвета это белый и черный, и три найденный треугольника покрашены в белый цвет. Заметим. что вершины, дополняющие каждый треугольник до квадрата должны быть окрашены в черный (иначе мы бы уже нашли квадрат). Но тогда посмотрим на обведенную точку. Легко видеть, что независимо от ее цвета мы найдем требуемый квадрат.