Принцип крайнего, индукция и другие методы в комбигео
Ошибка.
Попробуйте повторить позже
На плоскости отмечено 100 точек общего положения (т.е. никакие три не лежат на одной прямой). Докажите, что можно выбрать три
отмеченные точки 
, 
, 
так, чтобы для любой точки 
из оставшихся 97 отмеченных точек, прямые 
и 
не содержали бы
точек, лежащих внутри треугольника 
.
Источники:
Применим принцип крайнего: выберем среди всех троек точек треугольник 
с самым большим углом 
Предположим, что точки 
, 
, 
не подходят. Тогда существует точка 
в объединении частей плоскости, одна из которых
заключена между прямыми 
и 
а другая — между прямыми 
и 
При этом 
не может лежать внутри треугольника 
, иначе 
.
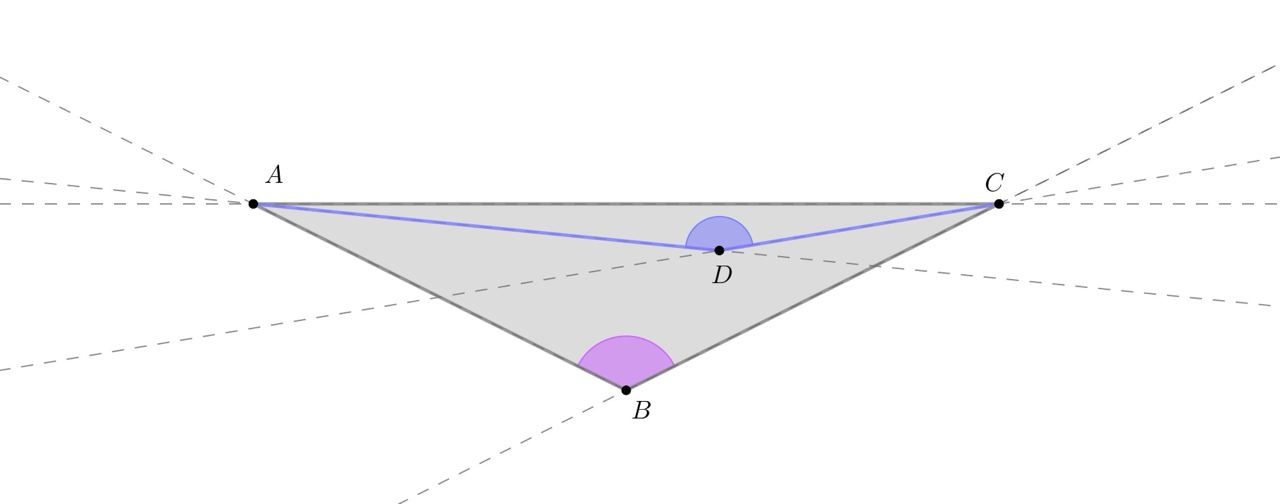
Рассмотрим случай, когда 
лежит между лучами 
и 
(когда 
и 
лежат в разных полуплоскостях относительно 
).
Тогда
получаем противоречие. То же работает для случая, когда 
лежит между лучами 
и 
.
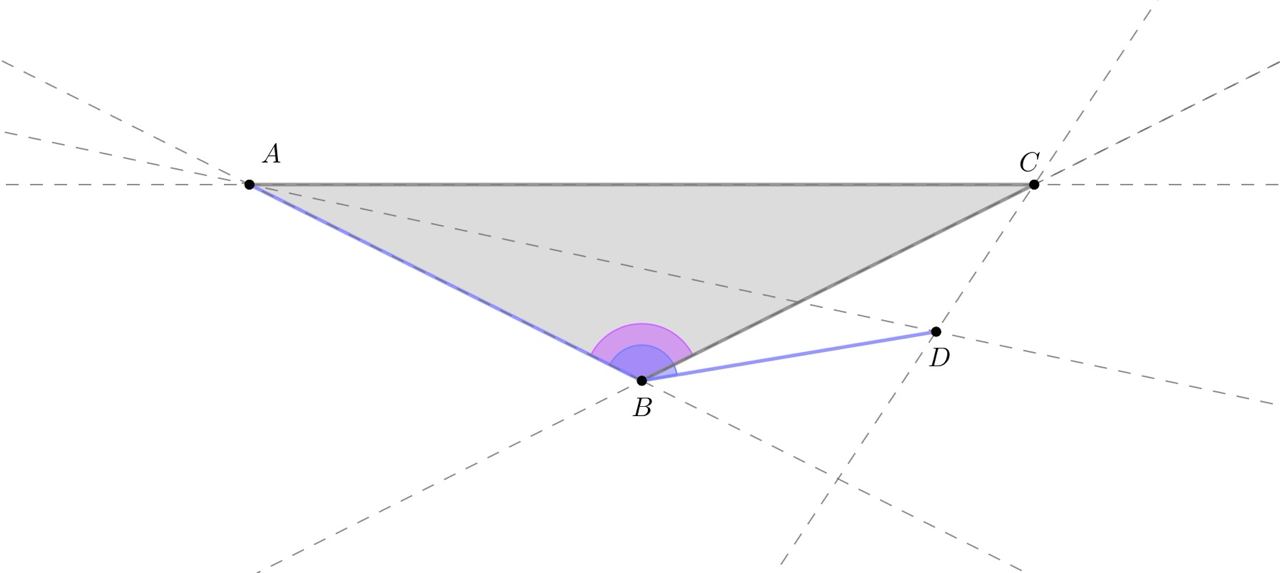
Оставшиеся два случая (когда 
и 
лежат в разных полуплоскостях относительно 
) рассматриваются аналогично: в
них
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
