18.29 Три неизвестные x,y,z

Первое уравнение при фиксированном задает окружность, центр которой лежит и радиус . Так как и , , то центр движется по верхней левой четверти окружности с центром в и радиусом . Следовательно, при всех первое уравнение задает голубую “колбаску”, состоящую из четверти области, заключенной между окружностями с центром в точке и радиусами и , а также двух полукругов с центрами в точках и :

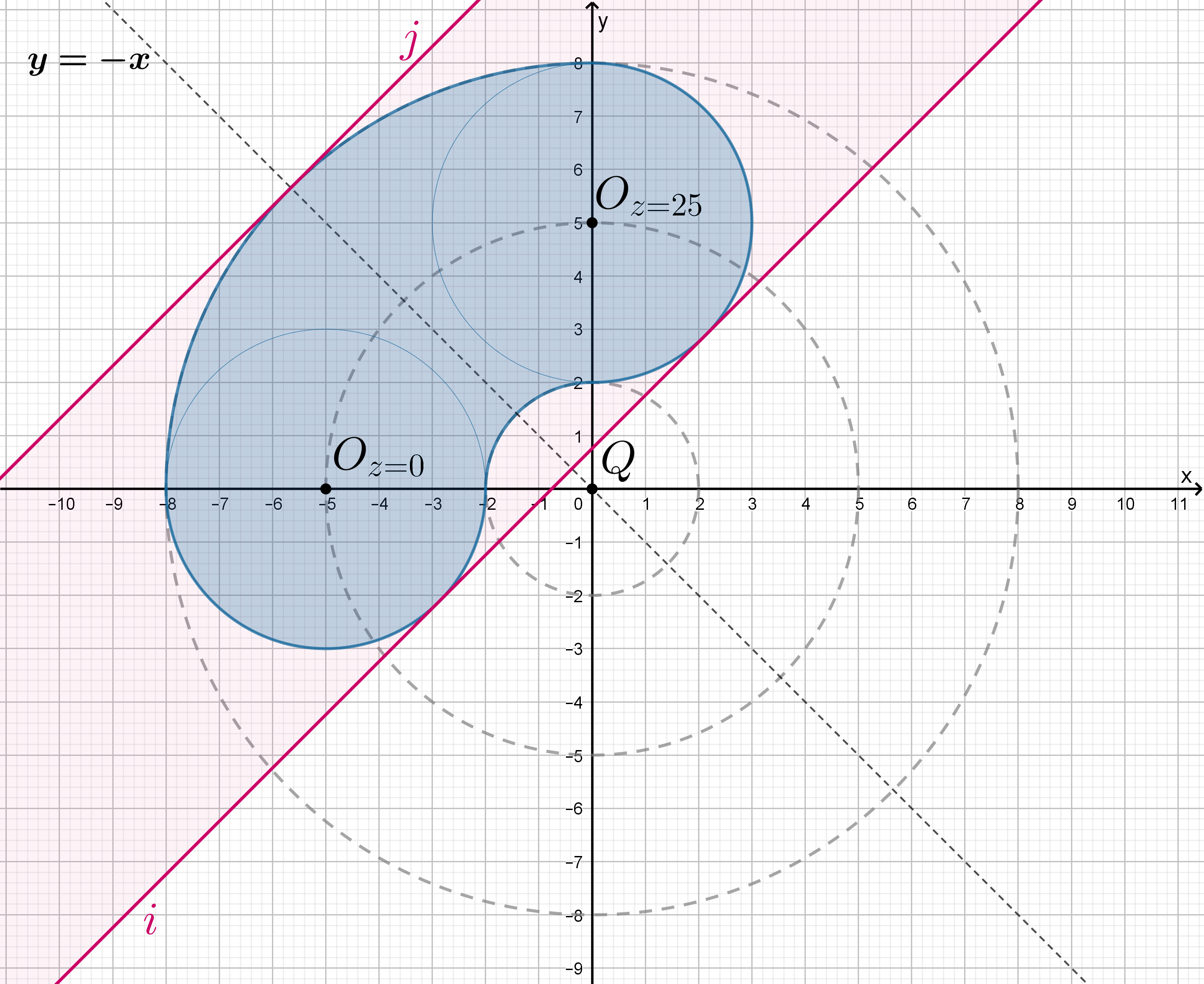
В розовой области находятся все положения прямой , при которых эта прямая с “колбаской” имеет хотя бы одну точку пересечения, то есть система имеет хотя бы одно решение (существует хотя бы одно , для которого существует такая окружность , которая имеет с прямой хотя бы одну точку пересечения ).

Заметим, что в силу симметрии голубой области и прямой относительно прямой , если прямая с окружностью для имеет точку пересечения, то она имеет и с окружностью для точку пересечения (положение ). А также в силу этой же симметрии положение задает прямую , точка пересечения которой с голубой областью единственна, следовательно, лежит на оси симметрии .

:

ищем через формулу расстояния от центра окружности до прямой, которое равно радиусу окружности (так как прямая касается окружности):

Нашему положению соответствует меньшее .

:

ищем через точку пересечения прямой и окружности во II четверти, то есть точку , которая лежит на , откуда

Следовательно,