18.09 Алгебра. Исследование замены

Пусть Тогда уравнение примет вид:

Проанализируем замену:

Полученное уравнение задает синусоиду:

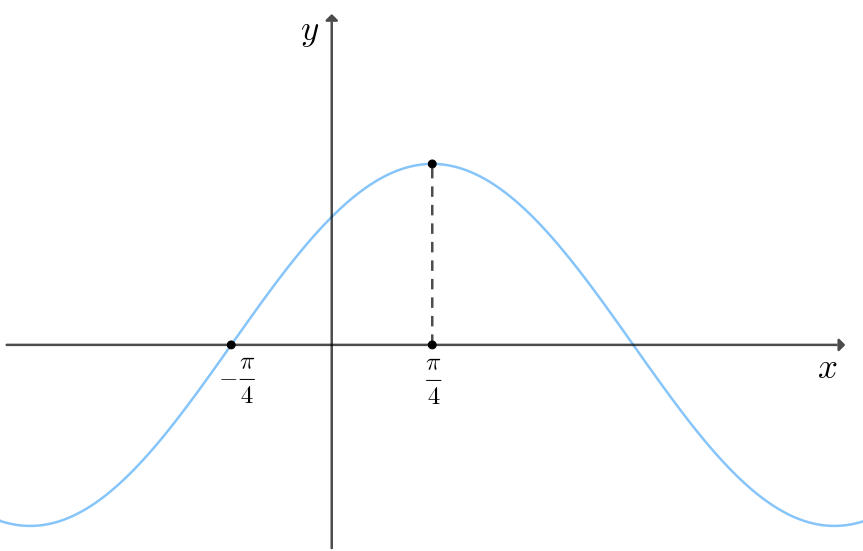
Обратим внимание, что на промежутке функция монотонно зависит от и принимает значения от до

Значит, одному решению уравнения будет соответствовать одно решение исходного уравнения.

Отсюда от уравнения мы требуем ровно два корня, лежащих на отрезке

Это уравнение либо квадратное, если либо линейное, если

Далее будем работать при

Пусть При необходимо выполнение следующих требований:

• тогда получаем следующее неравенство:

  

• тогда получаем следующее неравенство:

  

• тогда получаем следующее неравенство:

  

• тогда получаем следующее неравенство:

  

При получаем то же условие на вершину из которого следует Значит, этот случай невозможен.

Пересекая все найденные промежутки, получаем, что исходное уравнение имеет ровно два различных решения на указанном отрезке при