18.09 Алгебра. Исследование замены
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых уравнение
имеет хотя бы одно решение.
Сделаем замену и исследуем ее. Если взять за
то
и
Графиком функции является часть гиперболы при
. Чтобы
построить эту гиперболу, нужно гиперболу
сдвинуть на 1 влево и на 1
вверх. Тогда при
получим часть ветви:
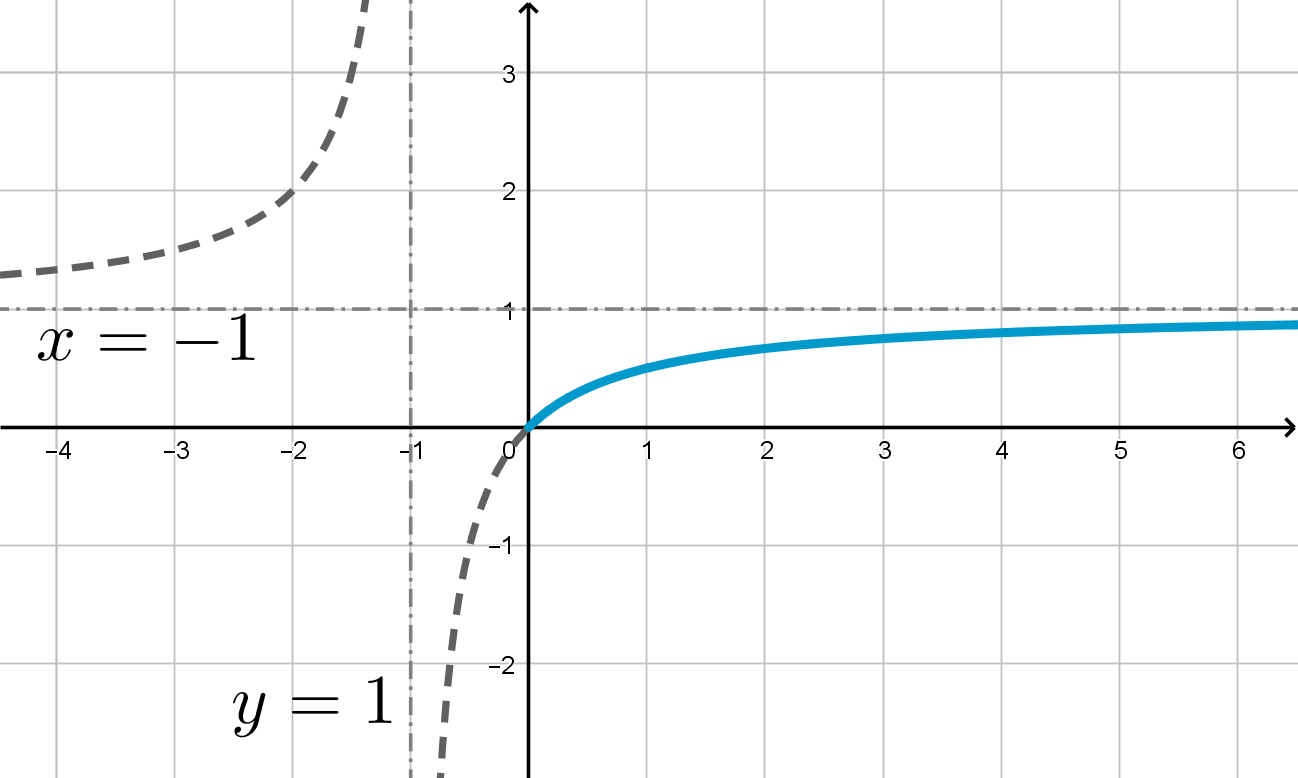
То есть Следовательно, исходное уравнение будет иметь хотя бы
одно решение, если уравнение
имеет хотя бы один корень из промежутка
Заметим, что это уравнение может вырождаться в линейное. Поэтому рассмотрим следующие случаи:
- 1)
Тогда уравнение примет вид
Следовательно, этот случай нам не подходит.
- 2)
Тогда уравнение квадратное и имеет решения, если его дискриминант неотрицателен:
- 2.1)
откуда
Тогда единственным корнем уравнения является абсцисса
вершины параболы, следовательно,
Из чисел
в этом промежутке лежит лишь число
То есть это значение параметра пойдет в ответ.
- 2.2)
откуда
Тогда, учитывая, что ветви параболы не зафиксированы и случай
мы рассмотрим отдельно, а также то, что при этих значениях параметра
(то есть оба корня не могут лежать в промежутке
), нам подходят следующие 4 случая:

то есть
Отсюда, так как произведение корней равно
получаем, что второй корень равен
Таким образом, этот случай нам не подходит, так как нет ни одного корня из промежутка
Пусть
Рассмотрим каждый рисунок в отдельности:
- 1:
- Ветви параболы направлены вверх, число 1 находится между
корнями, число 0 находится левее меньшего корня либо
совпадает с ним.
Эта ситуация задается следующей системой:
- 2:
- Ветви параболы направлены вниз, число 1 находится между
корнями, число 0 находится левее меньшего корня либо
совпадает с ним.
Эти две системы можно объединить в следующую:
- 3:
- Ветви параболы направлены вверх, число 1 находится правее
большего корня, число 0 находится левее большего корня либо
совпадает с ним.
Если найти множество
значений параметра, при которых число 0 находится правее большего корня при условии, что ветви направлены вверх, то при всех
число 0 находится левее большего корня или совпадает с ним (при выполнении всех условий тех случаев, в которых мы находимся, то есть при
И
). Тогда условие нашей картинки будет выглядеть следующим образом:
(1)
Найдем
Тогда система (1) равносильна:
Пересекая с
и
получаем значения параметра, идущие в ответ:
- 4:
- Ветви параболы направлены вниз, число 1 находится правее
большего корня, число 0 находится левее большего корня либо
совпадает с ним.
Аналогично предыдущему случаю (но ветви направлены вниз):
(2)
Найдем
Тогда система (2) равносильна:
Объединяя
с
получаем итоговый ответ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Не рассмотрен случай линейного
уравнения или случай | 3 |
| Верно
рассмотрен случай линейного уравнения и
| 2 |
| Введена и исследована замена, при этом может быть рассмотрен случай линейного уравнения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




