.20 Теорема о движении центра масс
Ошибка.
Попробуйте повторить позже
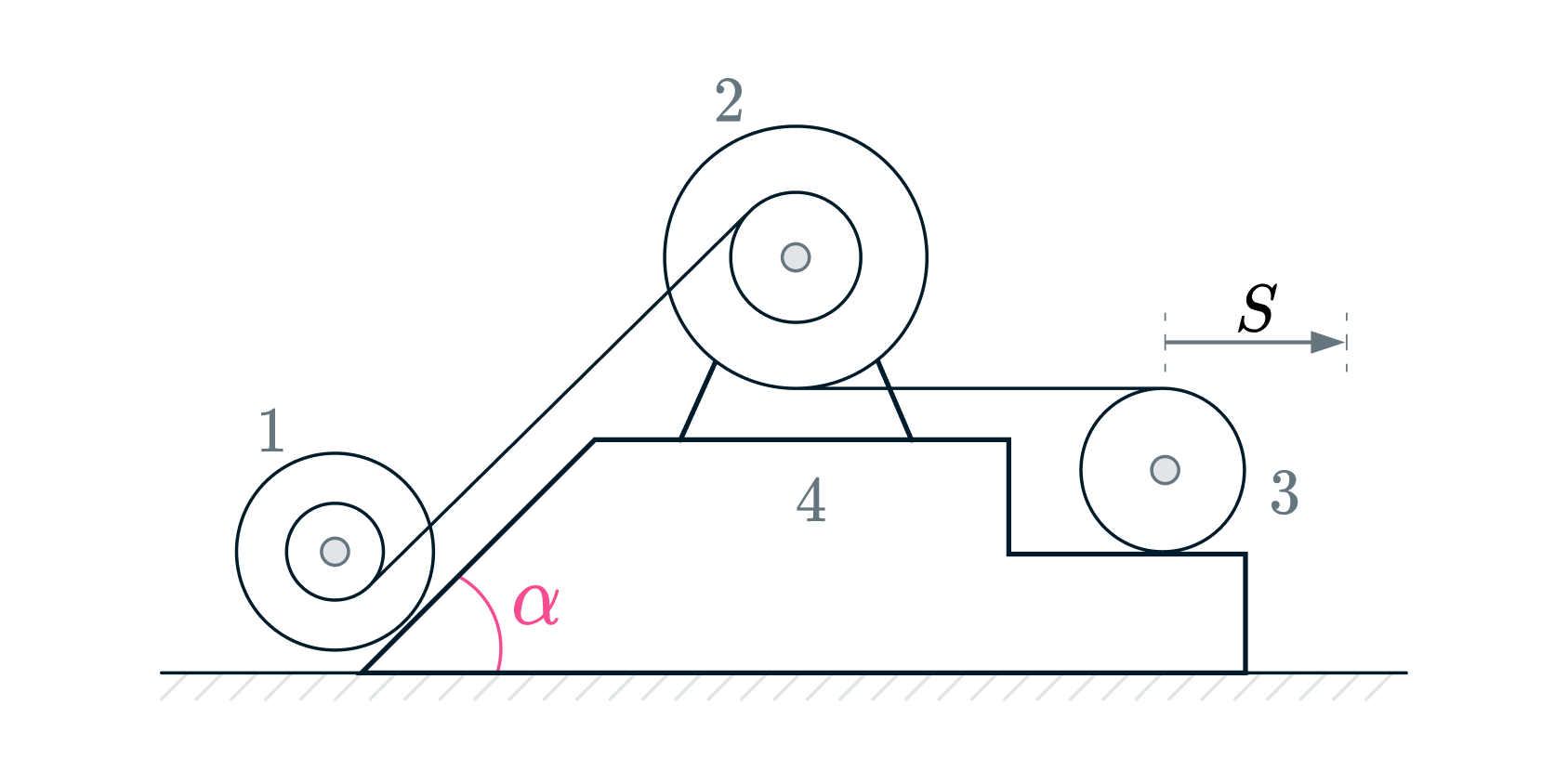
Механизм, состоящий из трех тел, установлен на призме 4, скользящей по гладкой плоскости (рис.).
Нить, соединяющая обод однородного цилиндра 3 с внешним радиусом составного блока 2, ось которого
закреплена на призме, горизонтальна. Внутренние радиусы блоков 1 и 2 соединены нитью, параллельной
плоскости призмы, по которой скатывается блок 1. Под действием внутренних сил из состояния
покоя механизм пришел в движение. Ось цилиндра 3 сместилась относительно призмы на
расстояние . Даны радиусы и массы
,
,
,
,
,
,
,
,
. Найти смещение призмы.
Из теоремы о движении центра масс системы следует , где
– ускорение центра масс
системы по оси
,
– масса всей системы. По условию задачи плоскость, по которой
скользит призма, гладкая. Трения и других внешних горизонтальных сил нет. Отсюда
и
. Интегрируя это уравнение при нулевой начальной скорости, получаем
. Еще раз
интегрируем:
Это означает, что в данном случае центр масс имеет постоянное положение.
Следовательно, с учетом формулы для координат центра масс, получаем
,
или
где ,
– смещения центров масс тел системы. Смещение каждого тела представим в
виде суммы относительного смещения
,
зависящего от заданного перемещения
оси
цилиндра 1, и переносного смещения призмы, которое обозначим за
и направим вправо. Таким
образом, в (3.24) входят абсолютные смещения
.
Рассмотрим относительные смещения тел. Смещение оси цилиндра 3 по условию задачи равно S.
Учитывая, что точка касания цилиндра и бруска в системе координат, связанной с призмой,
неподвижна, получаем, что верхняя точка обода этого цилиндра смещается на (рис. 241).
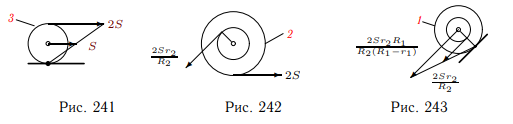
Нить, связывающая блок 2 и цилиндр 3 нерастяжима, поэтому нижняя точка внешнего обода блока 2
также сместится на 2S. При этом блок повернется на угол , а точка на внутреннем радиусе
блока сместится на
(рис. 242). Аналогично, вычислим угол поворота
блока 1 и, учитывая линейный характер распределения смещений в блоке 1 (рис. 243), получим
относительное смещение его оси
а в проекции на ось x с учетом, что смещение направлено налево, получим отрицательное смещение
В уравнение теоремы о движении центра масс войдет абсолютное смещение . Уравнение (3.24)
примет вид
Отсюда выражаем смещение призмы :
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




