.20 Теорема о движении центра масс
Ошибка.
Попробуйте повторить позже
Грузы массами и
(
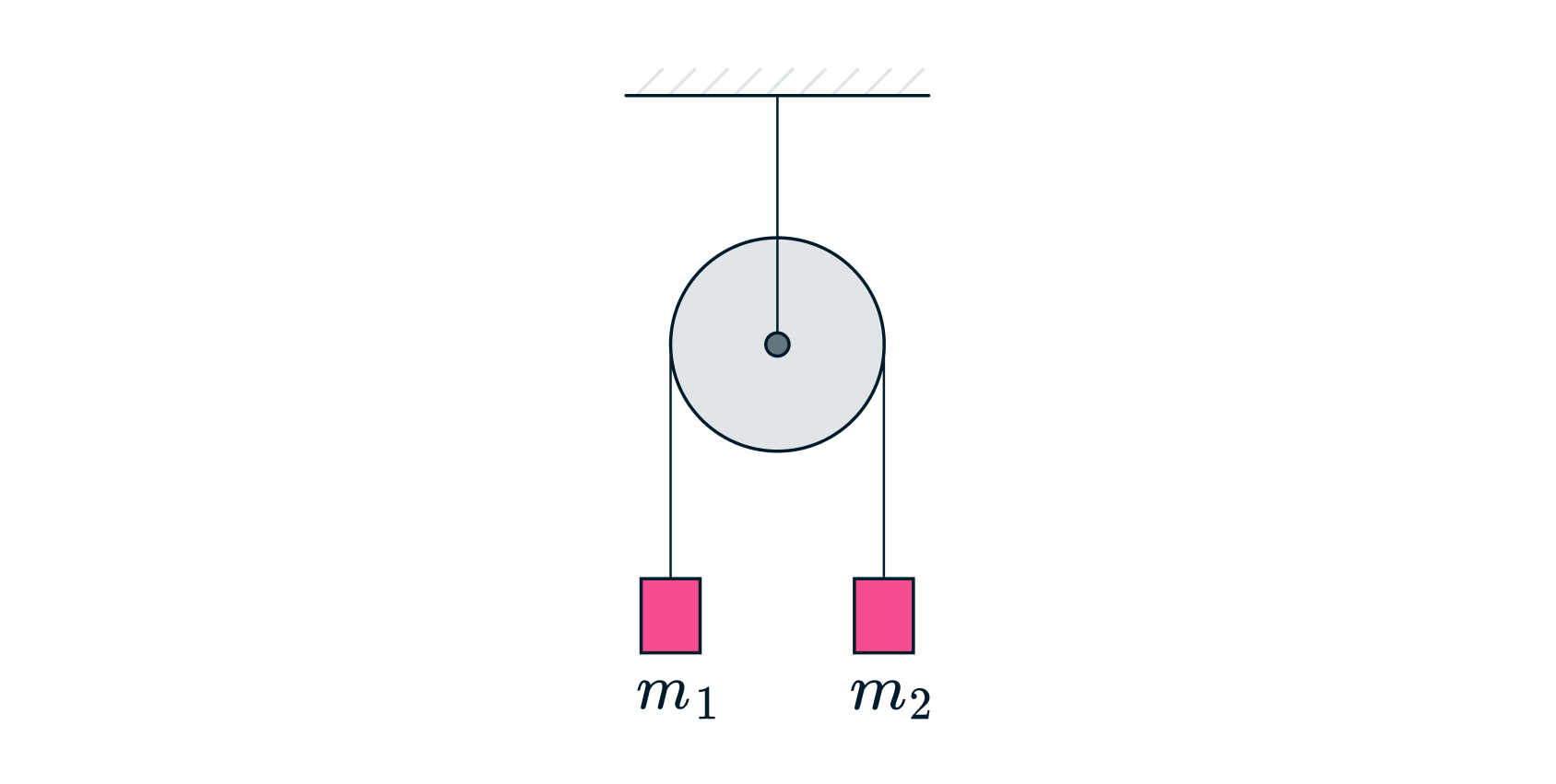
) прикреплены к нерастяжимой нити, перекинутой через
неподвижный блок (см. рисунок). Система предоставлена самой себе. Пользуясь теоремой о движении
центра масс, найдите вес системы
(силу давления на ось блока). Массами нити и блока пренебречь.
Трение в системе отсутствует.
(Машина Атвуда)
Так как нить невесома и нерастяжима, то сила натяжения всюду одинакова, а ускорения грузов равны по модулю. Запишем второй закон Ньютона в проекции на вертикальную ось
|
|
По теореме о движении центра масс
Вес, действующий на блок равен , значит
Или
| Критерии оценивания выполнения задачи | Баллы |
| Учащийся приступил к решению задачи | 1 |
| Написано краткое условие | 1 |
| Обосновано равенство сил натяжения, дейсвтующих на грузы, иравенство усорений грузов | 1 |
| Записан второй закон Ньютона для обоих грузов | 2 |
| Получено выражение для ускорения грузов | 1 |
| Записана теорема о движении центра масс | 1 |
| Получено выражение для ускорения центра масс ситсемы | 1 |
| Записан второй закон Ньютона для блока | 1 |
| Получено выражение для веса системы | 1 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




