.20 Теорема о движении центра масс
Ошибка.
Попробуйте повторить позже
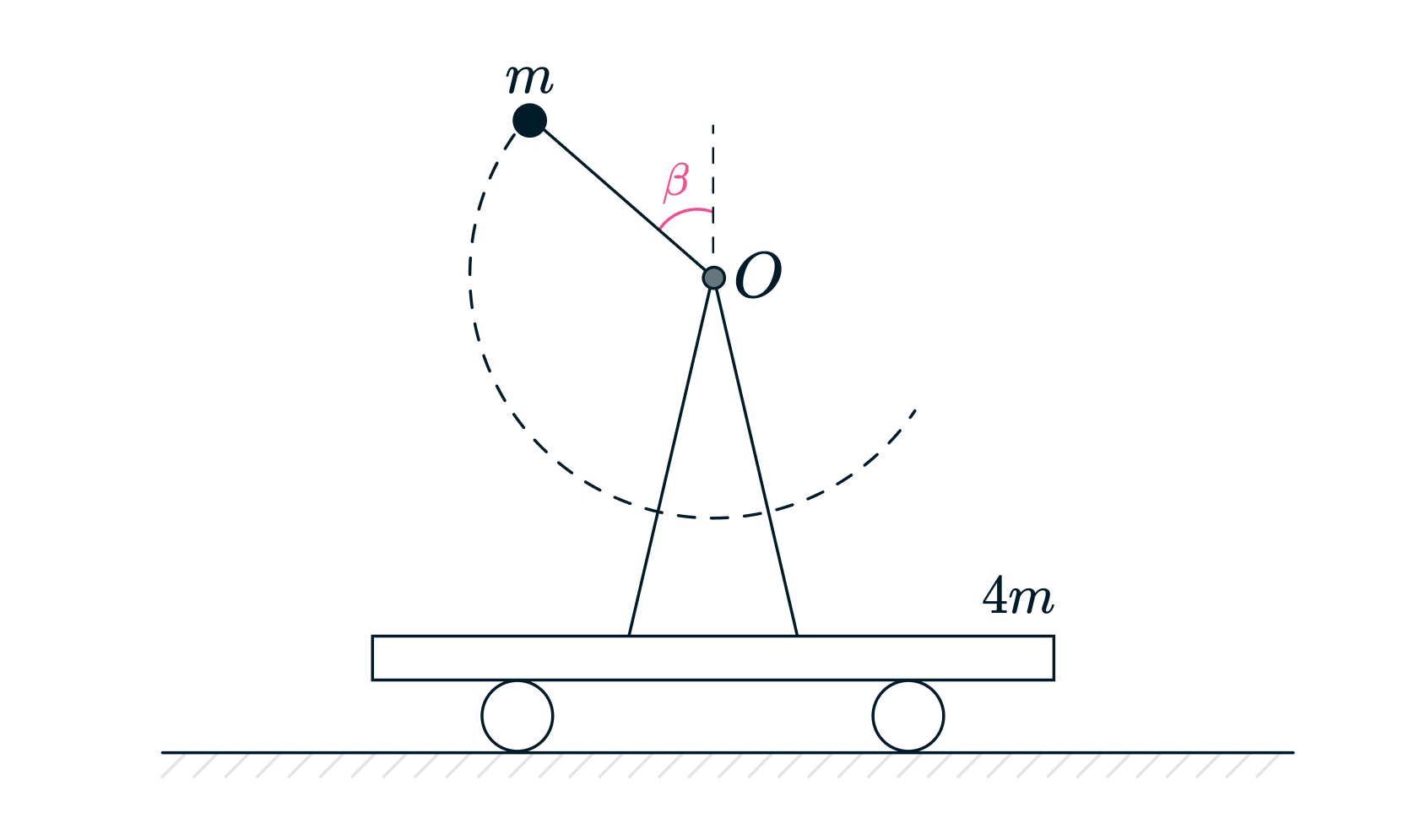
Тележка может двигаться прямолинейно, поступательно, без трения по горизонтальной поверхности
стола. К тележке прикреплена горизонтальная ось , перпендикулярная возможному направлению
движения тележки (см. рисунок). Вокруг оси
, в плоскости, перпендикулярной ей, может вращаться
без трения на стержне длиной
небольшой по размерам шарик массой
. Масса тележки,
оси O и её крепления равна
. Массами стержня и колёс тележки пренебречь. Вначале
тележка покоилась, а стержень удерживали под углом
к вертикали. Затем стержень
отпустили.
1) Найти скорость тележки при прохождении шариком нижней точки своей траектории.
2) Найти амплитуду колебаний тележки, то есть половину расстояния между наиболее удалёнными друг
от друга положениями тележки.
(МФТИ, 1999)
Источники:
1) В момент прохождения шариком нижней точки своей траектории его скорость горизонтальна и
направлена слева направо. Обозначим эту скорость через . Очевидно, что скорость тележки
направлена в противоположную сторону. Обозначим ее через
. Движение шарика, как и движение
тележки, мы рассматриваем в неподвижной системе координат. По закону сохранения энергии можно
записать
Здесь потенциальная энергия шарика отсчитывается от уровня, проходящего через нижнюю точку траектории шарика, поэтому в исходном положении шарик обладает только потенциальной энергией, а в нижней точке – только кинетической. Поскольку в горизонтальном направлении сумма действующих на систему тележка – шарик сил равна нулю, в любой момент времени импульс системы в горизонтальном направлении равен нулю:
Решая совместно систему двух уравнений, получим, что искомая скорость тележки равна
2) Так как горизонтальный импульс системы равен нулю, во время колебательных движений центр
тяжести нашей системы остается неизменным. Удаление тележки от центра тяжести будет
максимальным в тот момент, когда стержень находится в горизонтальном положении. Обозначим
расстояние (по горизонтали) от центра тяжести системы до центра тележки через , тогда
расстояние от шарика до центра тяжести системы будет
. По правилу моментов можно
записать
Отсюда амплитуда колебаний тележки будет равна
| Критерии оценивания выполнения задачи | Баллы |
| Учащийся приступил к решению задачи | 1 |
| Написано краткое условие | 1 |
| Записан закон сохранения энергии для системы "тележка + шарик" | 2 |
| Обоснован и записан аписан закон сохранения импульса для системы "тележка + шарик" | 2 |
| Получено выражение для скорости тележки | 1 |
| Описано движение центра масс системы "тележка + шарик" | 1 |
| Записано правило моментов | 1 |
| Получено выражение для амплитуды колебаний тележки | 1 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




