.20 Теорема о движении центра масс
Ошибка.
Попробуйте повторить позже
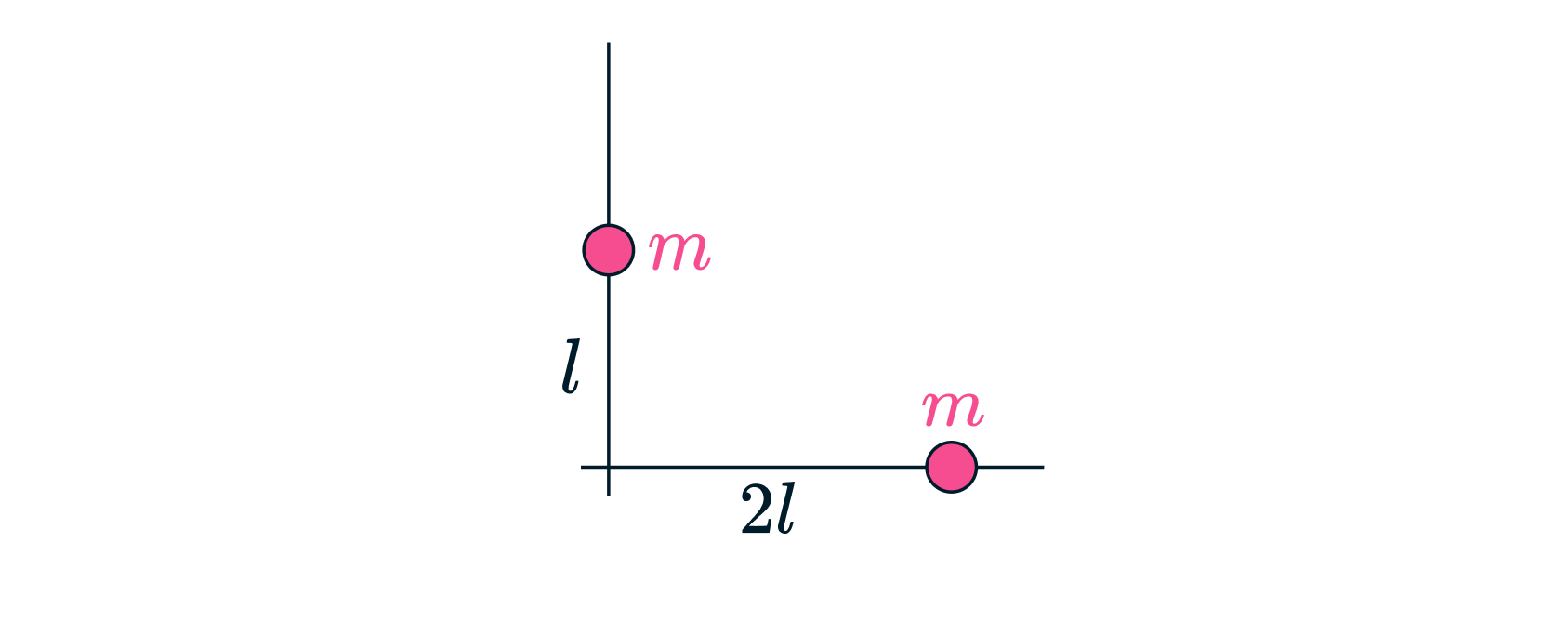
Два точечных тела с массами могут скользить по жёстким спицам, расположенным
под прямым углом друг к другу. Тела притягиваются с силой
, величина которой не
зависит от расстояния между ними. В начальный момент тела, которые удерживали на
расстояниях
и
от точки пересечения спиц, отпускают. Какое из них первым окажется в точке
пересечения спиц? Найти время его движения до этой точки. Силой тяжести и трением
пренебречь.
(«Росатом», 2014, 11)
Источники:
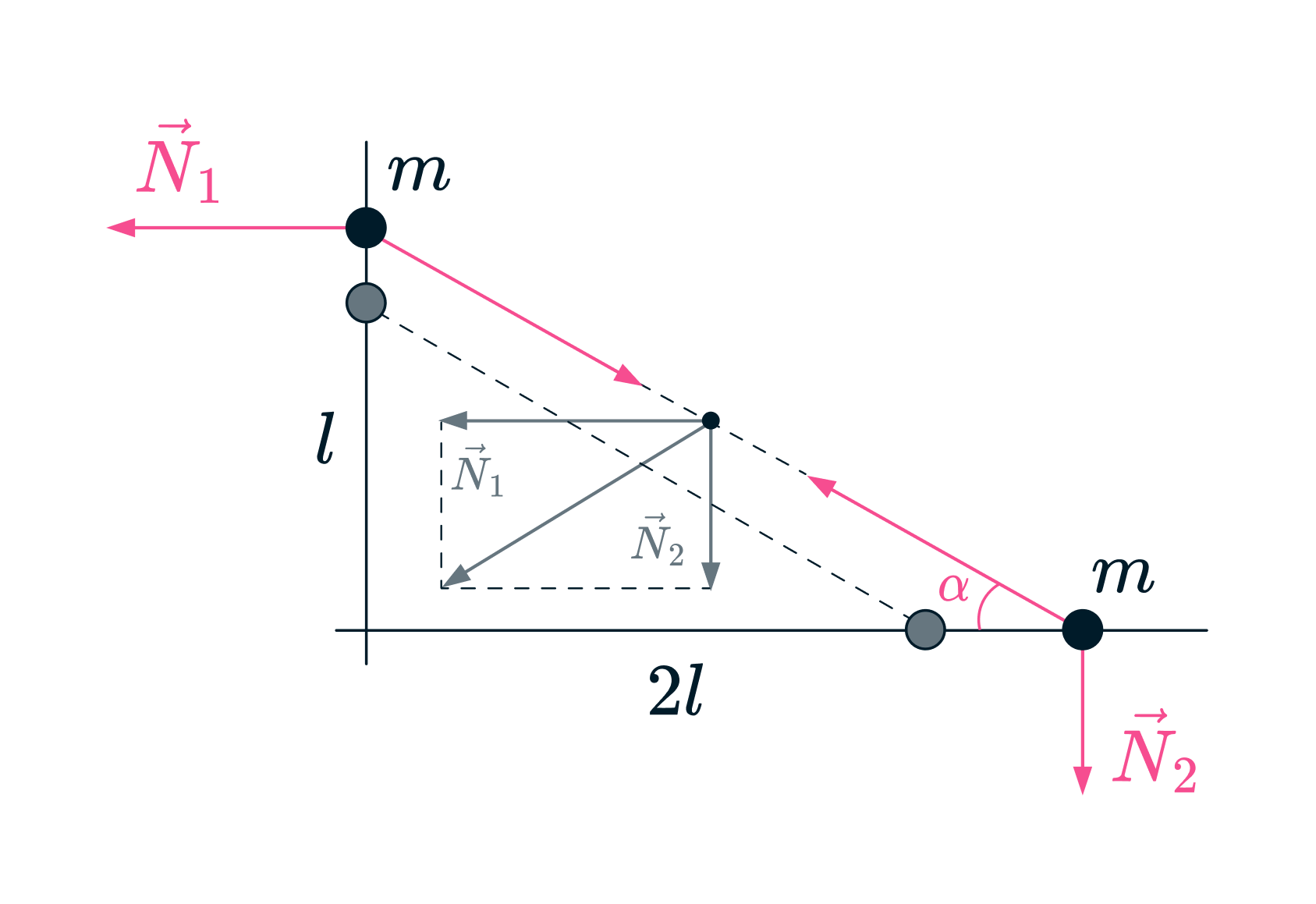
Внешними для системы двух шариков силами являются силы реакции стержней – и
,
которые находятся из условия нулевых проекций ускорения шариков на направения, перпендикулярные
стержням. В начальный момент, когда отрезок, соединяющий шрики, составляет угол
с
горизонтальным стержнем, эти силы равны
Центр масс системы (находится посередине между шариками) движется так, как будто в нем
сосредоточена вся масса системы (), и на него действует суммарная внешняя сила (
).
Геометрически очевидно, что в начальный момент эта сила направлена в точку пересечения стержней.
Это значит, что за некоторый малый интервал времени шарики переместятся так, что их центр масс
переместится точно в направлении точки пересечения стержней. А это значит что перемещения шариков
за этот интервал будут такими, что соединяющий их отрезок будет все время оставаться
параллельным самому себе, и центр масс все время будет двигаться вдоль прямой, соединяющей его
начальное положение и точку пересечения стержней. А это значит, что шарики попадут
в это точку одновременно. Время движения шариков можно найти так. Так как отрезок,
соединяющий шарики все время остается параллельным самому себе, то проекция силы
взаимодействия шариков на направление стержней не меняется. Поэтому движение шариков
равноускоренное. Применяя закон равноускоренного движения например к нижнему шарику,
получим
где
ускорение нижнего шарика. Отсюда находим
(Официальное решение Росатом)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




