.20 Теорема о движении центра масс
Ошибка.
Попробуйте повторить позже
Снаряд, летевший вертикально, взорвался в верхней точке своей траектории, распавшись на три осколка массами
,
и
, которые полетели в разные стороны с одинаковыми начальными скоростями. Через
некоторое время после взрыва расстояние между осколками
и
оказалось равным
. Чему было равно в этот
момент расстояние между осколками
и
, если ни один из осколков ещё не достиг земли? Влиянием воздуха и
массой взрывчатого вещества снаряда пренебречь.
(МОШ, 2007, 11)
Источники:
Перейдем в систему отсчета, падающую на землю с ускорением свободного падения . В этой системе отсчета осколки
после взрыва движутся в разные стороны равномерно и прямолинейно с одинаковыми скоростями, равными начальной
скорости
, приобретенной в результате взрыва. Из закона сохранения импульса следует, что начальные скорости
осколков лежат в одной плоскости. Следовательно, в рассматриваемой системе отсчета все осколки после взрыва снаряда в
любой момент времени располагаются на окружности с центром в точке взрыва. Изобразим эту окружность на рисунке,
обозначив угол между направлениями разлета осколков с массами
и
через
, а осколков с массами
и
– через
.
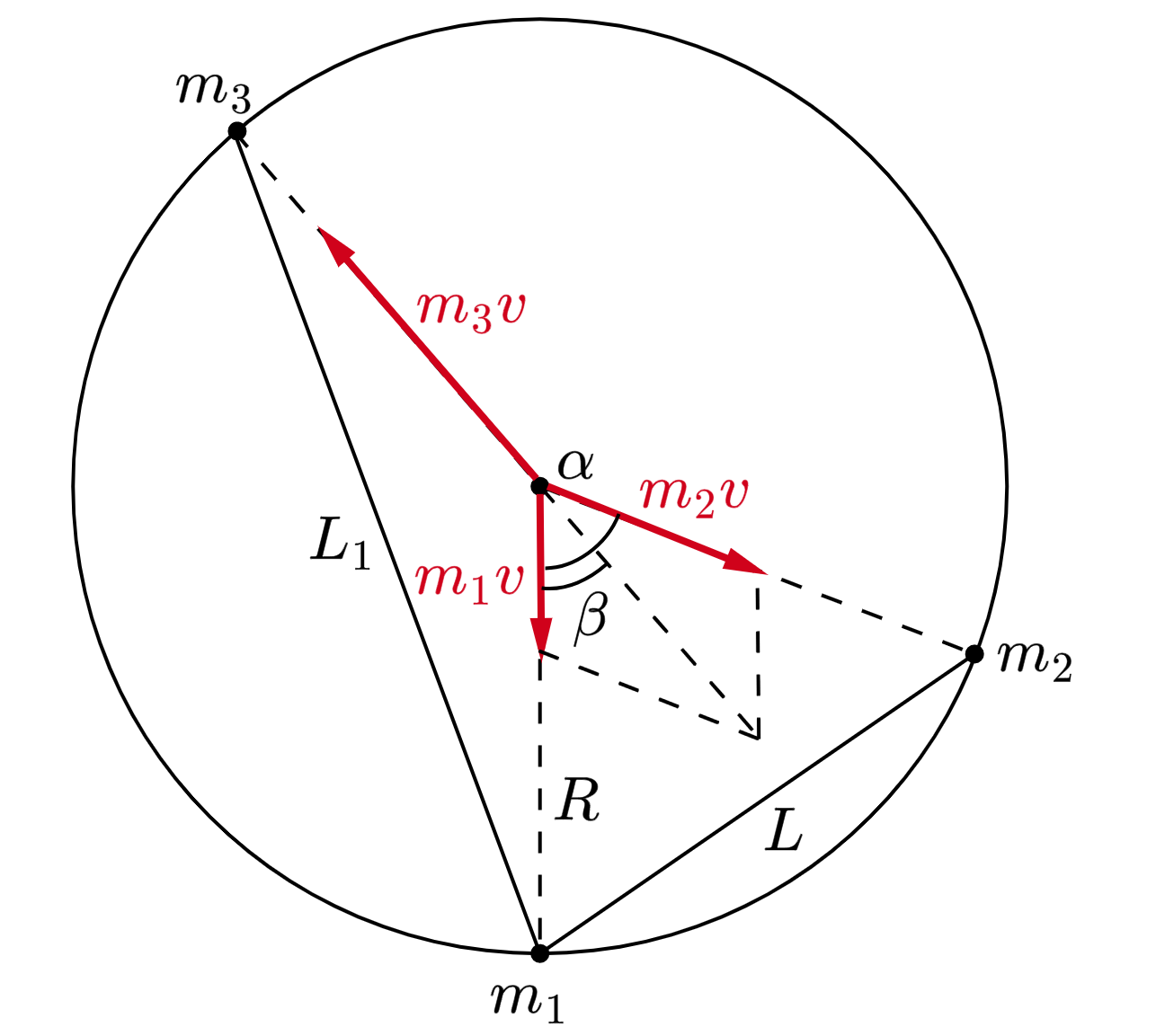
Рассмотрим положения осколков в момент времени, когда расстояние между первым и вторым осколками оказалось
равным . Тогда из рисунка следует, что
где – радиус изображенной окружности,
– искомое расстояние между первым и третьим осколками. Поскольку
импульс рассматриваемой системы осколков сохраняется, из теоремы косинусов, примененной к треугольнику из векторов
импульсов осколков, следует
Отсюда, с учетом заданных соотношений между ,
и
, находим
Из теоремы синусов, примененных к этому же треугольнику
Откуда
Используя тригонометрические формулы для половинного угла, найдем
Откуда Подставляя эти выражения в формулу для
, получим ответ:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




