.04 Закон сохранения и изменения энергии
Ошибка.
Попробуйте повторить позже
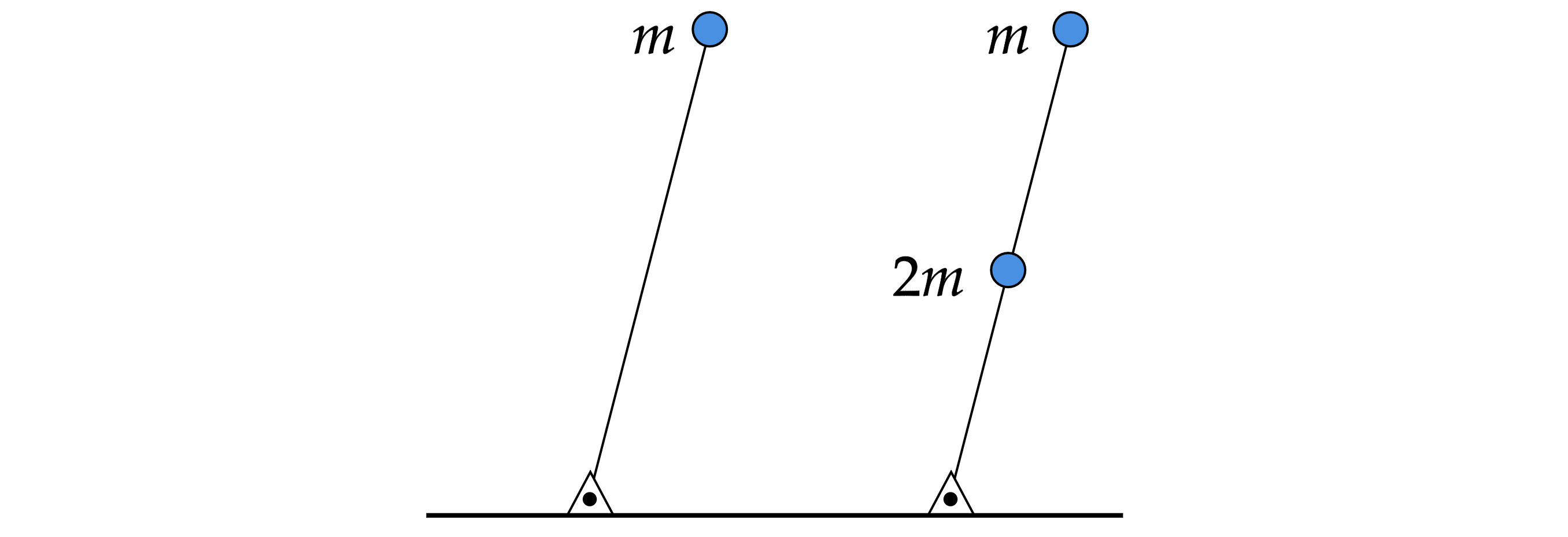
На конце невесомого стержня укреплено очень маленькое тело массой . Второй конец стержня
закреплен шарнирно на горизонтальной поверхности. Если расположить стержень под некоторым
углом к вертикали, а затем отпустить, он будет падать на поверхность в течение времени
. Какое время будут падать на поверхность стержень, если к его середине прикрепить
маленькое тело массы
, расположить под таким же углом к поверхности и отпустить?
(«Росатом», 2019, 11)
Источники:
Сравним угловые скорости стержней в тот момент, когда они будут расположены под некоторым углом
к поверхности. Итак, рассмотрим первый стержень (с одним телом). Когда он окажется под углом к
вертикали, убыль потенциальной энергии буде равна
где – начальный угол между стержнем и вертикалью (см. рисунок). Поэтому закон сохранения
механической энергии дает
где и
– скорость тела и угловая скорость стержня в тот момент, когда он будет наклонен под
углом
к поверхности. Отсюда находим
Рассмотрим теперь второй стержень в тот момент, когда он будет наклонен под углом
к поверхности (см. рисунок). Убыль потенциальной энергии для него будет определяться
выражением
А закон сохранения механической энергии для этого стержня дает
где – угловая скорость второго стержня в тот момент, когда он будет наклонен под углом
к
поверхности. Отсюда находим
Отсюда следует, что отношение времен, которые стержень затрачивает на прохождение каждого малого поворота равно
И не зависит от угла . Это значит, что и отношение полных времен движения такое же.
Или
(Официальное решение Росатом)
Второй способ решения:
Система представляет собой физический маятник. Вращательное движение стержня с грузами
описывается уравнением динамики вращательного движения
где - момент силы относительно некоторой точки;
- момент инерции системы относительно некоторой точки;
- угловое ускорение.
Рассмотрим уравнение динамики вращательного движения относительно точки крепления. Как
известно, момент инерции точечной массы на расстоянии от оси вращения выражается
формулой
Тогда аналогично для второго стержня
Будем считать,что время падения не зависит от угла, поэтому углы отклонения от положения
равновесия будем считать малыми.
Моменты силы относительно точки опоры тогда будут равны
Тогда получаем следущие уравнения вращательного движения
Тогда угловые ускорения
Угловое ускорение связано с временем падения. Для малых углов движение можно приблизить
гармоническим осциллятором, где период связан с угловой частотой
. Вспомним уравнения
гармонического осциллятора
Время падения ( четверть периода)
Тогда для первой ситуации
Для второй
| Критерии оценивания выполнения задачи | Баллы |
| Описан и записан закон ссохранения механической энергии для первого стержня | 2 |
| Получено выражение для угловой скорости первого стержня | 2 |
| Описан и записан закон ссохранения механической энергии для первого стержня | 2 |
| Получено выражение для угловой скорости первого стержня | 2 |
| Описано соотношение времен | 1 |
| Поулчено выражение для искомого времени | 1 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




