.04 Закон сохранения и изменения энергии
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
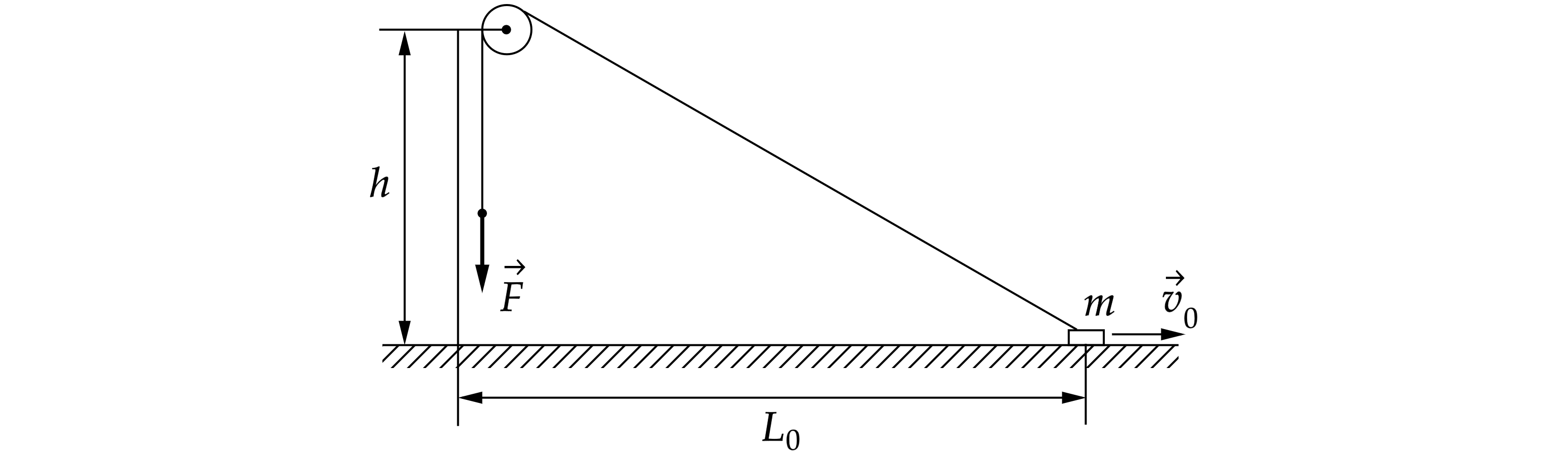
Маленький брусок массой 
находится на гладкой горизонтальной поверхности на расстоянии 
от вертикального
столба, на котором на высоте 
на коротком держателе закреплён маленький невесомый блок с неподвижной
горизонтальной осью. Лёгкая нерастяжимая длинная нить одним концом прикреплена к бруску, перекинута через блок и
натянута с постоянной силой 
. Трения в оси блока нет. В начальный момент брусок скользит по поверхности и
имеет скорость 
, направленную от столба. Какой будет скорость бруска в тот момент, когда брусок перестанет давить
на поверхность?
(«Курчатов», 2016, 11)
Источники:
Из условия задачи ясно, что в начальный момент брусок давит на горизонтальную поверхность, то есть «оторваться» от
поверхности он сможет только на обратном пути к столбу, когда расстояние 
станет меньше, чем 
. Кинетическая
энергия бруска изменяется, так как сила 
совершает работу. Поскольку сила, действующая на брусок всегда направлена
вдоль нити к блоку, то работа равна произведению величины силы на изменение длины участка нити между бруском и
блоком, взятому со знаком минус.
В момент, когда брусок перестанет давить на поверхность, на брусок будут действовать только сила натяжения нити и
сила тяжести. Поскольку ускорение бруска будет всё ещё направленно по горизонтали, сумма вертикальных проекций
действующих на брусок сил будет равна нулю:
Скорость 
бруска в этот момент найдём из закона изменения механической энергии:
(Официальное решение Курчатов)
| Критерии оценивания выполнения задачи | Баллы |
| Указано, что работа силы | 2 |
| Найдено расстояние от блока до бруска в момент, когда брусок перестанет давить на поверхность | 1 |
| Записан закон изменения механической энергии | 1 |
| Представлен правильный ответ | 1 |
| Максимальный балл | 5 |
равна произведению величины силы на изменение длины участка нити между бруском и блоком, взятому со знаком
минус 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
