.04 Закон сохранения и изменения энергии
Ошибка.
Попробуйте повторить позже
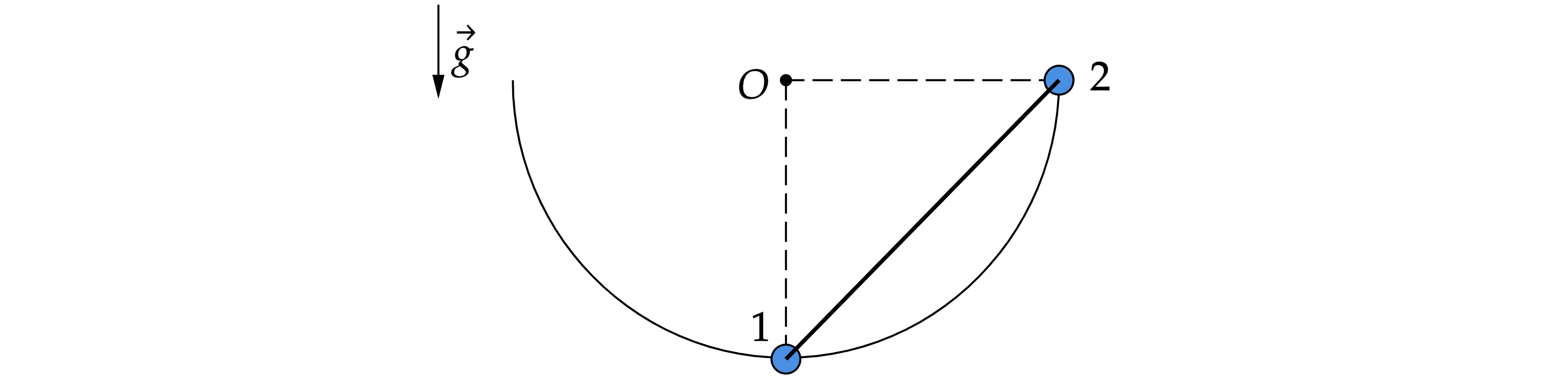
Из тонкой проволоки согнута полуокружность с центром в точке и радиусом
. Полуокружность неподвижно
закреплена в вертикальной плоскости. По проволоке могут скользить без трения маленькие бусинки 1 и 2,
соединённые жёстким невесомым стержнем. Отношение масс бусинок
. При движении стержень
может свободно поворачиваться вокруг точек крепления к бусинкам. В начальном положении бусинки 1
и 2 находятся на концах вертикального и горизонтального радиусов. Стержень с бусинками отпускают
без толчка. Найдите максимальную скорость
бусинки 1 при дальнейшем движении. Бусинки считайте
материальными точками. Ускорение свободного падения
. Ответ выразите в м/с и округлите до
сотых.
(«Курчатов», 2019, 11)
Источники:
Рассмотрим промежуточное положение системы, когда радиусы, проведённые из центра полуокружности
к бусинкам, повернулись на угол относительно своих первоначальных положений. Скорости бусинок
обозначим через
и
. Отсчитывая высоты от центра полуокружности, запишем закон сохранения
энергии:
Здесь – радиус полуокружности,
. Так как длина стержня не меняется при движении, то проекции
скоростей на направление стержня совпадают. Из простых геометрических соображений следует, что при любом значении
угла
скорости бусинок образуют со стержнем углы в
Получаем:
Исключая скорость , находим
как функцию угла
:
Функция равна:
Преобразуем эту функцию с помощью метода вспомогательного аргумента:
Вспомогательный аргумент определяется двумя равенствами:
Угол лежит в первой четверти. Поэтому его можно выразить через арктангенс:
Очевидно, что функция максимальна при
:
Тогда максимальная скорость первой бусинки равна:
Ответ также можно представить в виде, удобном для приближённого вычисления:
Следует отметить, что угол определяет положение равновесия системы. Действительно, приравнивая моменты сил
тяжести относительно центра полуокружности, получаем:
Поскольку бусинки совершают колебания около положения равновесия, можно сразу считать очевидным, что максимальные скорости достигаются в этом положении.
(Официальное решение Курчатов)
| Критерии оценивания выполнения задачи | Баллы |
| Записан второй закон Ньютона | 2 |
| Представлено доказательство равенства скоростей | 2 |
| Верно определен центр масс | 2 |
| Верно записан закон сохранения энергии, найден верный угол отклонения шариков | 2 |
| Правильно получена конечная формула, нет логических ошибок, получен правильный численный ответ | 2 |
| Максимальный балл | 10 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




