.17 Силы инерции. НСО
Ошибка.
Попробуйте повторить позже
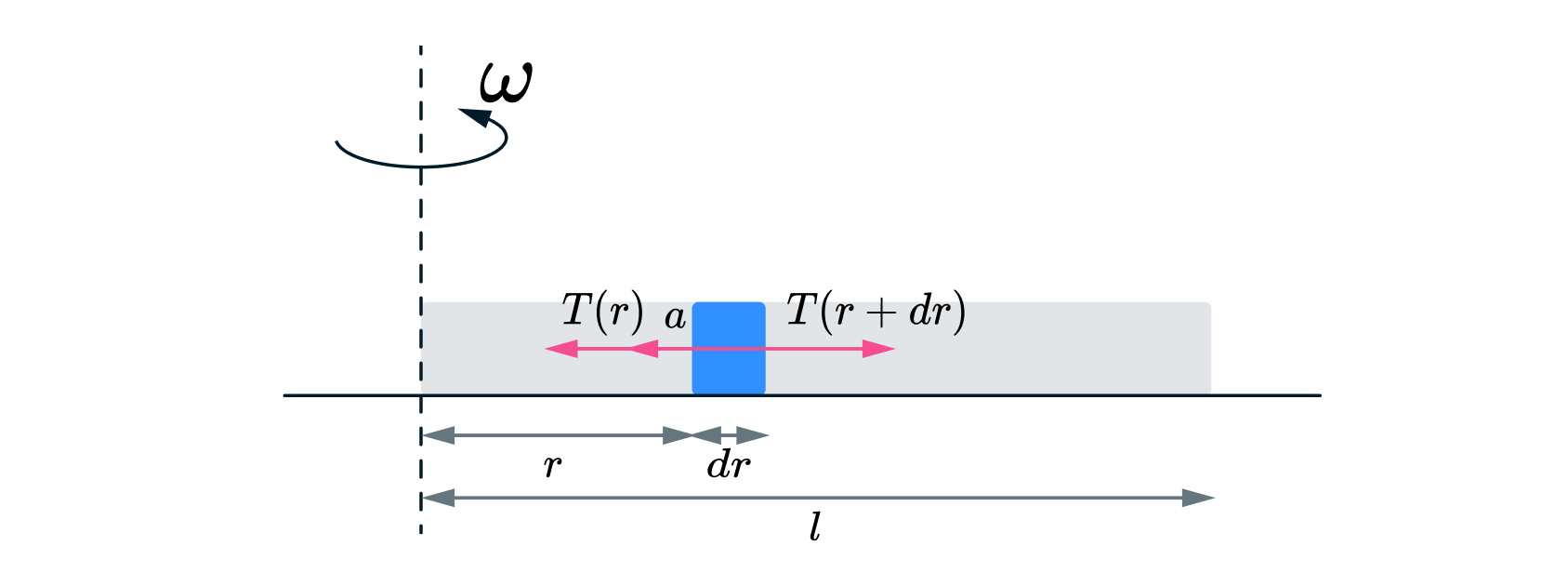
Веревку длиной и массой
, расположенную на гладком горизонтальном столе, вращают с угловой скоростью
вокруг одного из её концов (см. рисунок). Найти силу натяжения веревки в сечении, находящемся на расстоянии
от
оси вращения.

(Росатом 2025, 11)
Мысленно разобьём верёвку на такие малые элементы, что каждый можно считать находящимся на определённом
расстоянии от оси вращения. Тогда второй закон Ньютона для этого элемента верёвки массой и длиной
, который
находится на расстоянии
от оси вращения:
где и
— силы натяжения верёвки с двух сторон от рассматриваемого элемента. При этом масса
элемента может быть представлена как:
Интегрируя уравнения движения для всех элементов верёвки, находящихся на расстояниях от до
от оси
вращения, получим следующее. Сумма разностей сил натяжения даст силу натяжения верёвки
в сечении, находящемся
на расстоянии
от оси вращения. Т.к. сила натяжения верёвки на самом её конце равна нулю, а все
промежуточные значения сократятся при суммировании (т.е. как раз ту величину, которую мы и должны
найти).
Интеграл левой части:
Получаем:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




