Симедианы
Ошибка.
Попробуйте повторить позже
Две окружности пересекаются в точках 
и 
. Из произвольной точки 
(не совпадающей с точками 
и 
) одной окружности
проводятся прямые 
и 
, пересекающие вторую окружность в точках 
и 
соответственно. Докажите, что для всех
получающихся треугольников 
(при фиксированных точках 
, 
и при выборе произвольной точки 
) их медианы, проведённые
из вершины 
, либо все пересекаются в одной точке, либо попарно параллельны.
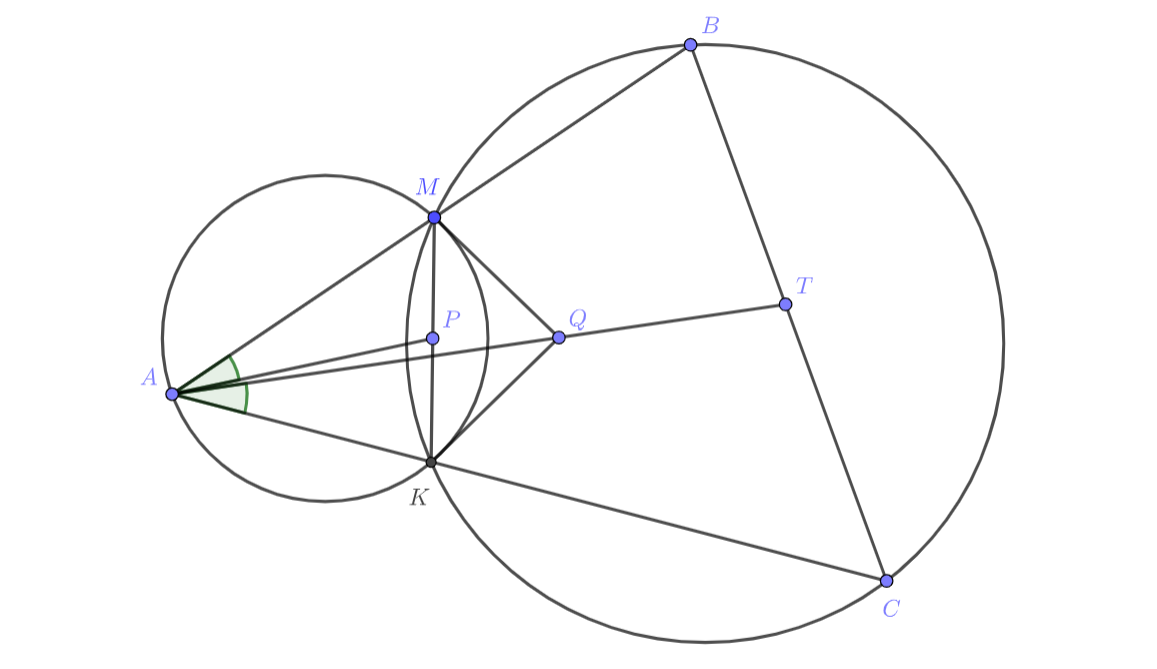
Если 
— медиана 
и 
— медиана 
, то 
, поскольку 
вписан и 
. Отсюда
— симедиана 
.
- Если
проходит через центр первой окружности, то 
. Как мы знаем, симедиана прямоугольного
треугольника является высотой. Тогда все симедианы треугольника 
перпендикулярны прямой 
, значит, все
медианы треугольника 
параллельны между собой.
-
Если
не проходит через центр первой окружности, то 
проходит через точку пересечения касательных к первой окружности
из точек 
и 
. Эта точка не зависит от выбора точки 
, потому всевозможные медианы треугольника 
пересекаются в
одной точке. 
что и требовалось доказать
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
