Симедианы

Первое решение. Пусть — основание перпендикуляра из точки на прямую По свойству прямоугольного треугольника то есть прямые и антипараллельны в угле Осталось заметить, что является симедианой треугольника а значит, медианой для любого треугольника, третья сторона которого антипараллельна в указанном угле.

Второе решение. Обозначим через вторую точку пересечения прямой и а через — середину Касательные к в точках и пересекаются на прямой откуда следует, что четырёхугольник гармонический.

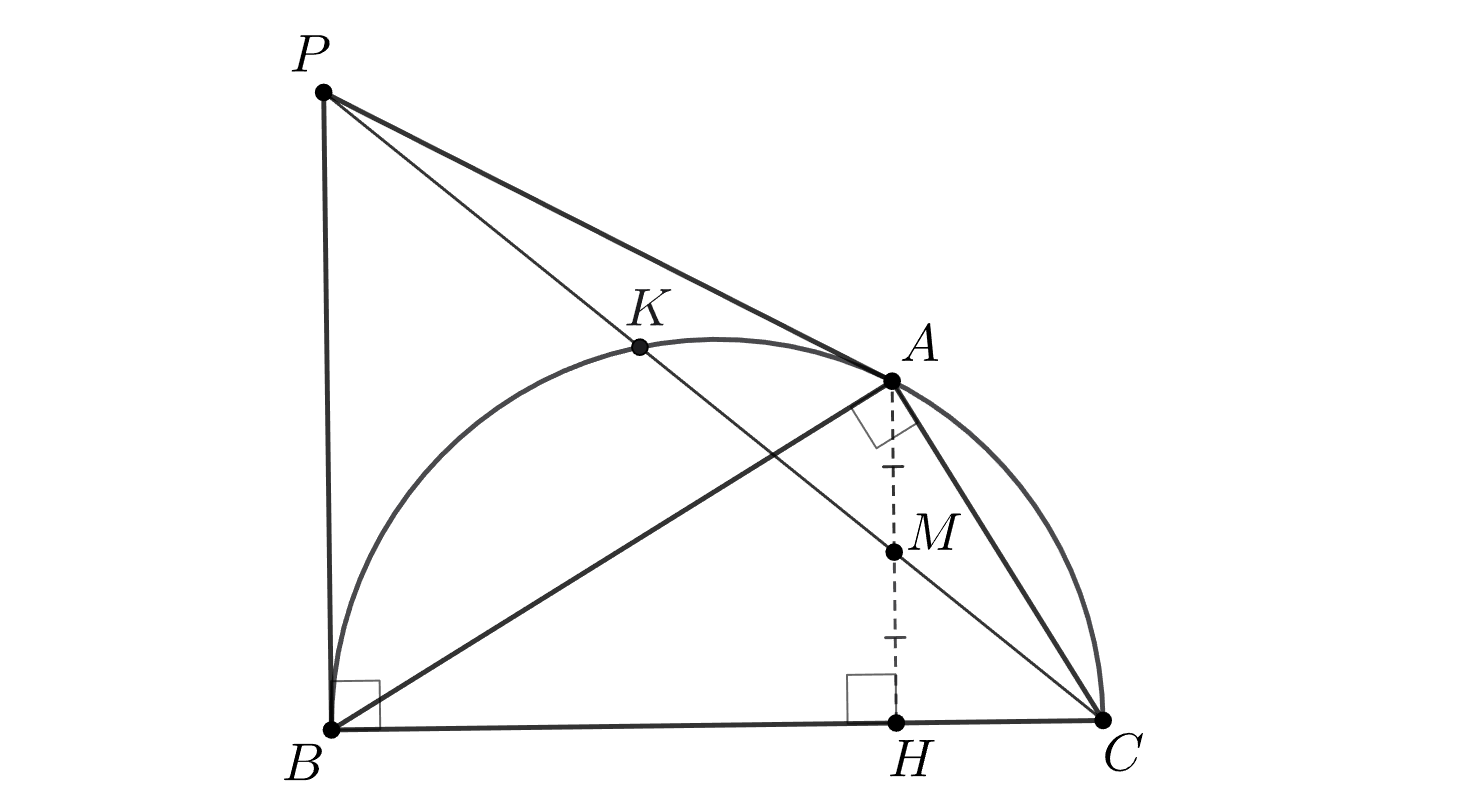
Делая проекцию четвёрки точек из точки на прямую получаем, что

Предпоследнее равенство следует из того, что касательная в точке к параллельна прямой так как она перпендикулярна диаметру как и прямая Значит, является серединой

______________________________________________________________________________________________________________________________________________________

Замечание. Из доказанного факта следует, что точка Лемуана прямоугольного треугольника совпадает с серединой его высоты, проведенной из прямого угла.