Симедианы
Ошибка.
Попробуйте повторить позже
проведены высоты 
, 
и 
. Точка 
— середина 
. Докажите, что:
к описанной окружности треугольника 
параллельна прямой 
;
и 
касаются описанной окружности треугольника 
Подсказка 1
У нас на картинке есть касательная к описанной окружности. Какой теоремой, связывающей уголочки, мы можем воспользоваться?
Подсказка 2
Конечно теоремой о угле между касательной и хордой! А именно: угол между касательной и хордой AB равен углу ACB. А что мы можем сказать про четырехугольник BCB₁C₁?
Подсказка 3
На самом деле он вписан, ведь углы BC₁C и BB₁C равны 90° и смотрят на отрезок BC. Осталось воспользоваться фактом, что во вписанном четырехугольнике сумма противоположных углов равна 180° и дело в шляпе!
Подсказка 4
Давайте докажем, что уголочки BB₁M и B₁AA₁ равны, тогда из обратной теоремы об угле между касательной и хордой мы получим, что MB₁ касается описанной окружности треугольника AB₁C₁.
Подсказка 5
Начнем с уголочка B₁AA₁. Что мы можем сказать о четырехугольнике AB₁A₁B?
Подсказка 6
Он вписан, т.к. уголки AB₁B и AA₁B равны 90°. Тогда B₁AA₁ равен углу B₁BA₁, т.к. они опираются на дугу B₁A₁. Теперь осталось доказать, что B₁BA₁, который равен B₁BM, равен BB₁M...
Подсказка 7
Если это так, то треугольник BMB₁ должен быть равнобедренный. А это действительно так, ведь медиана В₁M, проведенная из вершины прямого угла, равна половине основания ВС, а значит B₁M=BM. Теперь осталось провести аналогичные рассуждения для углов C₁AA₁ и МС₁С и завершить решение задачи.
(a) Отметим на касательной точку 
по свойству угла между хордой и касательной. В свою очередь
в силу вписанности четырехугольника 
следовательно 
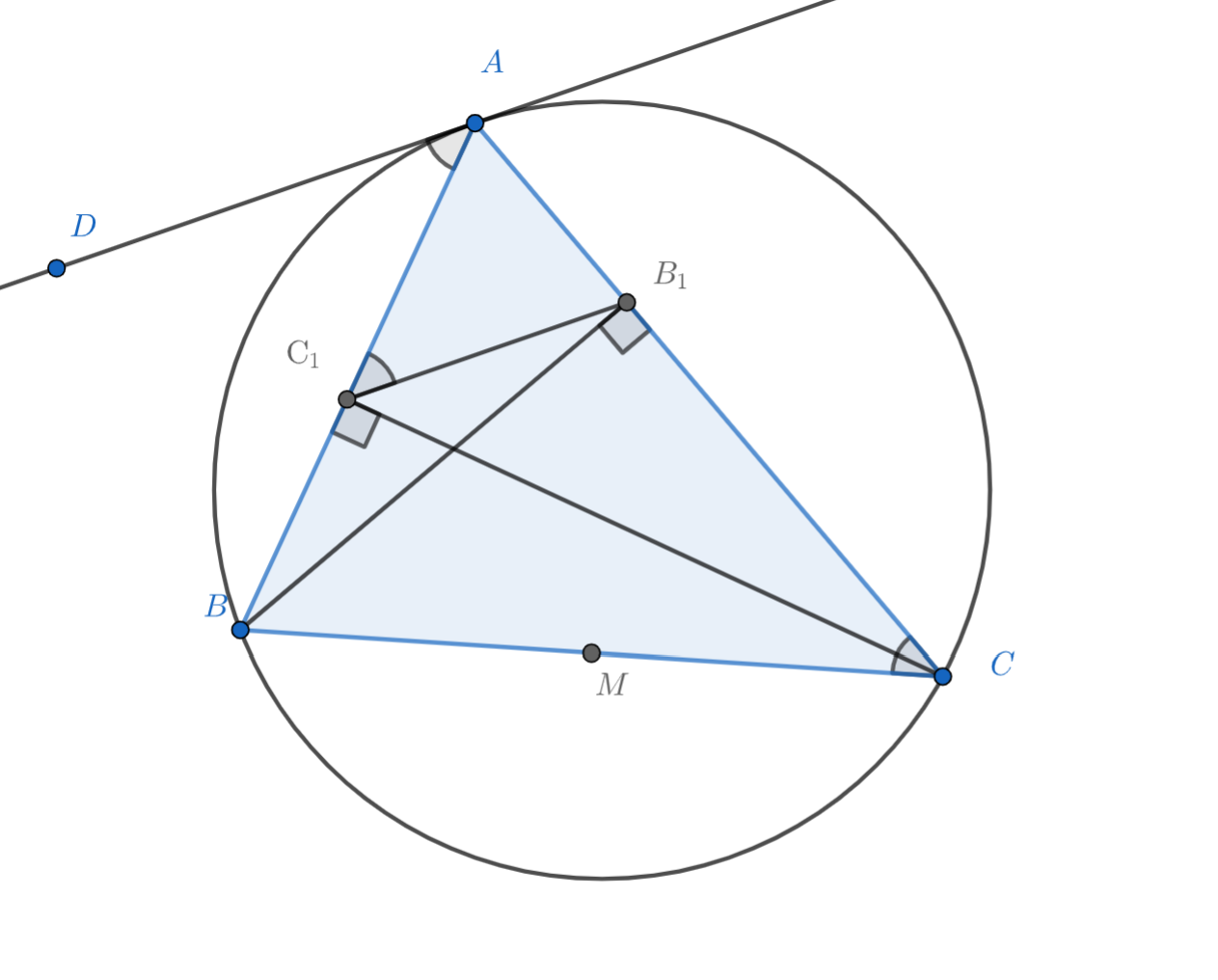
(b) Чтобы доказать, что прямые 
и 
касаются описанной окружности треугольника 
докажем, что
и 
— углы между 
и хордами 
соответственно.
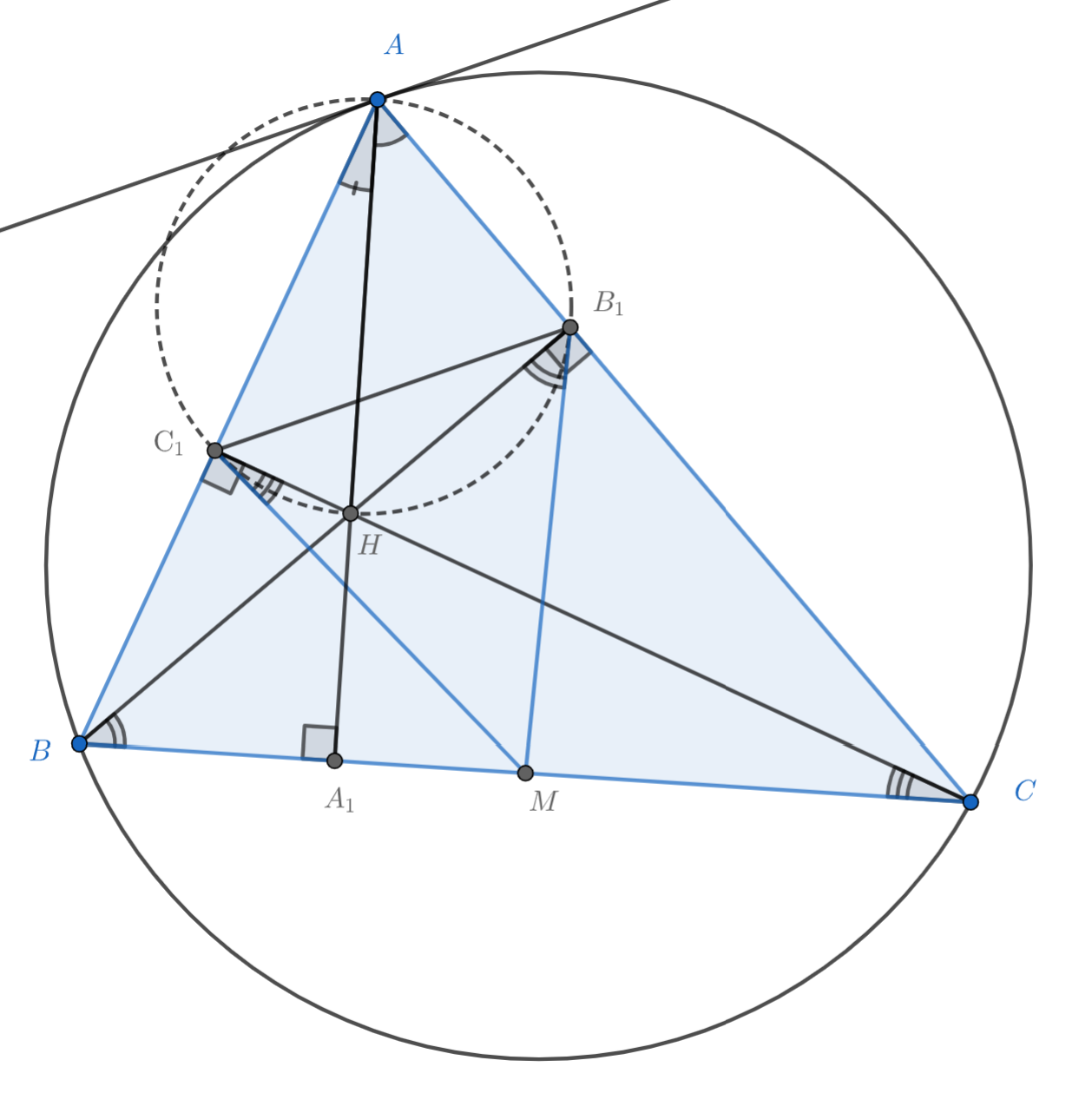
Так как 
— вписанный, точка 
лежит на окружности, описанной около треугольника 
Так как 
— середина 
, то 
по свойству медианы прямоугольных треугольников 
и
Пусть 
Тогда 
и следовательно 
и тогда 
Итого 
—
касательная к окружности, описанной около треугольника 
Аналогично доказывается для 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
