18.25 Графика. Области
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых система
имеет ровно два решения.
В первом уравнении системы оба слагаемых левой части неотрицательны при всех значениях и
Сумма этих
слагаемых равна нулю тогда и только тогда, когда каждое из них равно нулю. Таким образом, исходная система
равносильна
В первом уравнении преобразованной системы имеем стандартную параболу во втором — линейную функцию
Линейная и квадратичная функции имеют не более двух точек пересечения, а по условию нас просят найти
при которых решений ровно два. Значит, нас интересуют значения
при которых обе эти точки пересечения являются
решениями системы.
Условие означает, что никакие точки вертикальной прямой
не могут быть решениями системы.
Четвертое условие означает, что нас интересуют только положительные значения
Последнее условие задает область между вертикальными прямыми
и
(включая эти прямые, так
как знаки нестрогие).
Таким образом, чтобы система имела ровно два решения, обе точки пересечения функций и
должны лежать в области
причем ни одна из них не должна принадлежать «запрещенной» вертикальной прямой
Построим графики (на
картинке область
изображена при
):
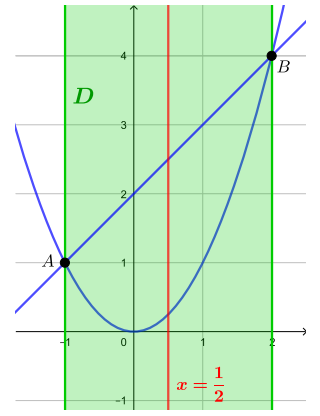
Графики и
пересекаются в точках
и
Ни одна из них не лежит на прямой
- При
левая граница
области
обращается в
и проходит через точку
а правая граница
области
обращается в
и проходит через точку
то есть обе точки принадлежат области
такие
нам подходят.
- При всех
область
становится «уже» и точка
оказывается левее прямой
а точка
— правее прямой
то есть точки
и
не попадают в область
такие
нам не подходят.
- При всех
обе точки
и
лежат внутри области
Таким образом, нам подходят
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточно обоснованное построение/недостаточно обоснован какой-то момент при исследовании | 3 |
| ИЛИ | |
| ответ отличается от верного невключением граничной точки | |
| Верно найдены точки пересечения и граничное значение параметра, но переход к ответу неверный | 2 |
| ИЛИ | |
| допущена вычислительная ошибка | |
| Верно сведено к исследованию графически или аналитически и выполнено верное построение с обоснованием | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




