Планиметрия на ОММО
Ошибка.
Попробуйте повторить позже
На одной из сторон острого угла с вершиной взяты точки
и
, а на другой – точка
. При какой длине отрезка
величина
угла
максимальна, если
Подсказка 1
В таких задачах бывает полезно сделать какие-то дополнительные построения, на рисунке ведь почти ничего полезного нет. Какую конструкцию хочется добавить на картинку, чтобы одновременно и воспользоваться длинами отрезков, и было что-то связанное с углами?
Подсказка 2
Кажется, какие-то прямые строить не хочется, иначе уйдём в тяжёлый счёт, пытаясь связать длины отрезков с углами. Может быть, у нас есть на примете какие-то кривые?
Подсказка 3
Тут неплохим вариантом кажется построение окружности через точки A и B, касающейся другой стороны угла.
Подсказка 4
Кажется, что точка касания стороны угла и окружности и будет той самой точкой C, при которой угол ACB — максимален. Давайте попробуем это доказать.
Подсказка 5
Если мы возьмём точку, отличную от точки касания, то предполагаемый угол будет отсекать от окружности две дуги. Как градусная мера угла связана с градусными мерами этих дуг?
Подсказка 6
Такой угол равен полуразности большей и меньшей дуг, которые он отсекает. А значит, будет меньше угла ACB, где C — точка касания окружности и прямой. Осталось лишь найти величину отрезка OC.
Проведем через точки и
окружность, касающуюся второй стороны угла. Если
— точка касания, то угол
равен половине
дуги
В противном случае угол
равен полуразности дуги
и второй дуги, высекаемой углом
— т. е. будет меньше.
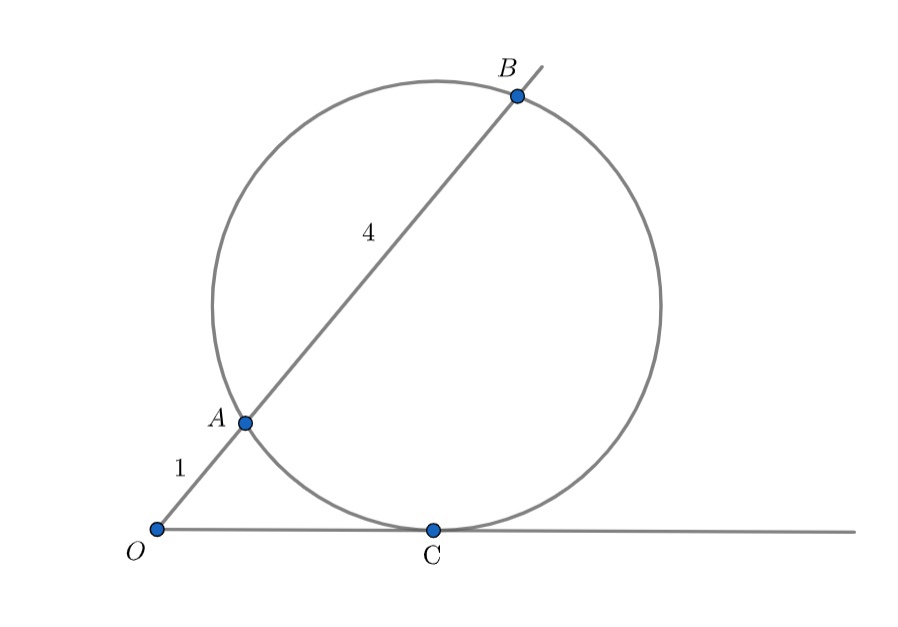
Остается воспользоваться тем, что квадрат касательной равен произведению секущей на ее внешнюю часть, откуда
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




