Планиметрия на ОММО

Первое решение.

Пусть — высота/медиана/биссектриса треугольника. Пусть — пересечение луча и отрезка .

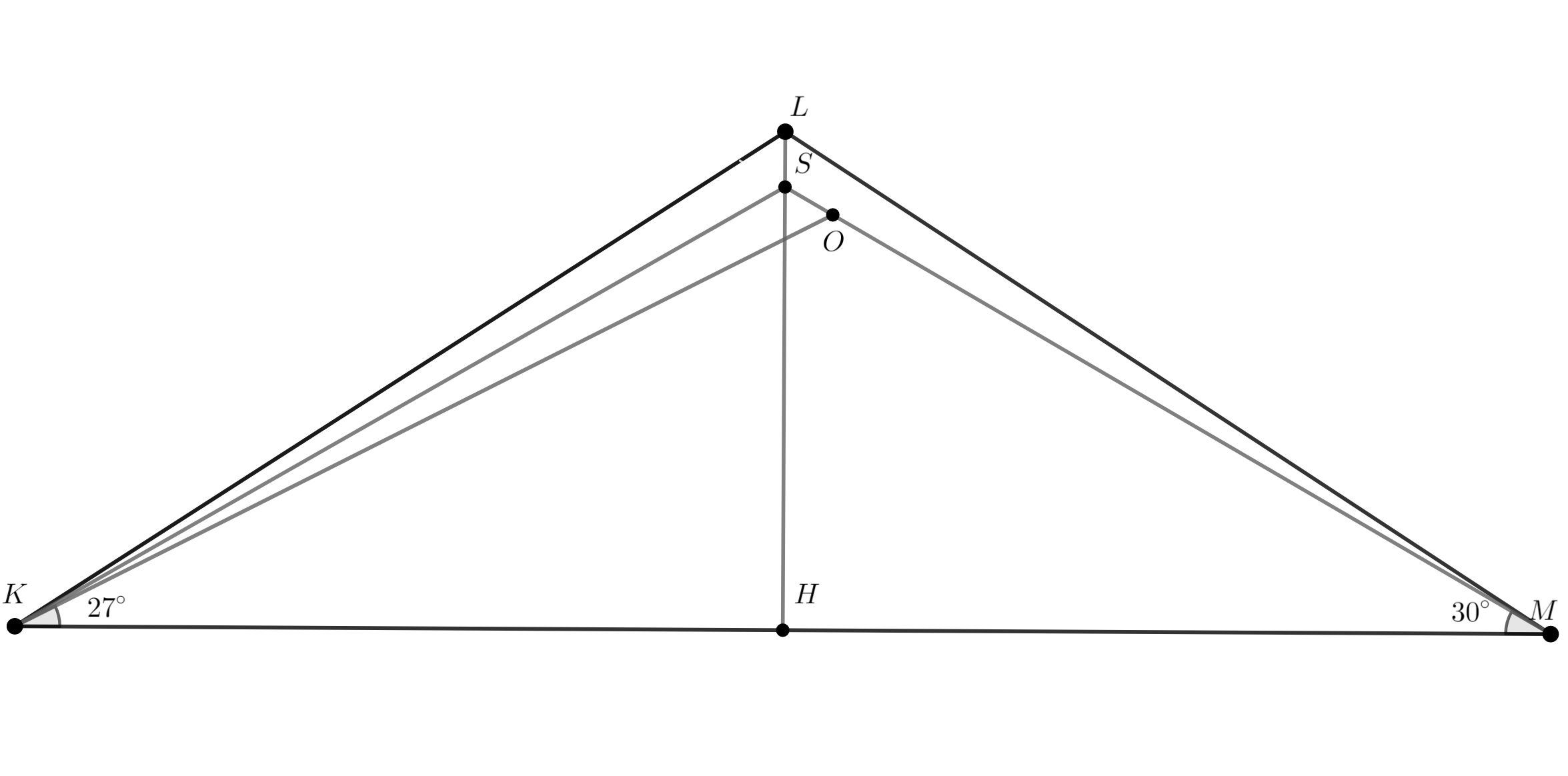
Заметим, что (поскольку в треугольнике медиана совпала с высотой).

Посчитаем углы: 1. ; 2. ; 3. ; 4. ; 5. , а значит ; 6. , а значит .

Треугольники и равны по общей стороне и двум углам (пункты 5. и 6.) Следовательно, , треугольник равнобедренный. Значит,

________________________________________________________________________________________

Второе решение.

Несложно посчитать, что . Докажем, что , а . Для этого воспользуемся тригонометрической формой теоремы Чевы. В соответствии с этой теоремой нам достаточно проверить, что

или . Это очевидно:

Осталось лишь вычислить из треугольника .