Стереометрия на ОММО
Ошибка.
Попробуйте повторить позже
Про тетраэдр известно, что
Вокруг тетраэдра описана сфера. Рассмотрим на этой сфере множество всех точек, сумма сферических расстояний от которых до точек
не меньше
. Чему равна площадь этого множества?
Замечание. Сферическое расстояние между двумя точками на сфере — длина наименьшей дуги окружности большого круга, соединяющей эти точки.
Источники:
Подсказка 1
Давайте обратим внимание на треугольники PRS и QRS. Они же прямоугольные. А что можно сказать про середину гипотенузы RS и про сферу?
Подсказка 2
Давайте обратим внимание на сумму сферических расстояний от точки R до некоторой точки M и от точки M до S. Кажется, в прошлом пункте мы поняли, что RS — диаметр сферы (если не поняли, срочно вернитесь к прошлой подсказке и поймите). На каких окружностях круга лежат пары точек M, R и S, R? Они различные?
Подсказка 3
Итак, осталось показать, что сумма сферических расстояний M, P и M, Q не меньше 3π. Давайте сделаем следующий трюк. Рассмотрим точку Q₁, симметричную Q относительно центра сферы. Как можно её использовать?
Подсказка 4:
По рассуждениям из предыдущих подсказок сумма сферических расстояний Q, M и M, Q₁ равна 3π. Значит, нужно доказать, что расстояние точек M, P не меньше расстояния точек M, Q₁. Осталось немного подумать и добить задачу.
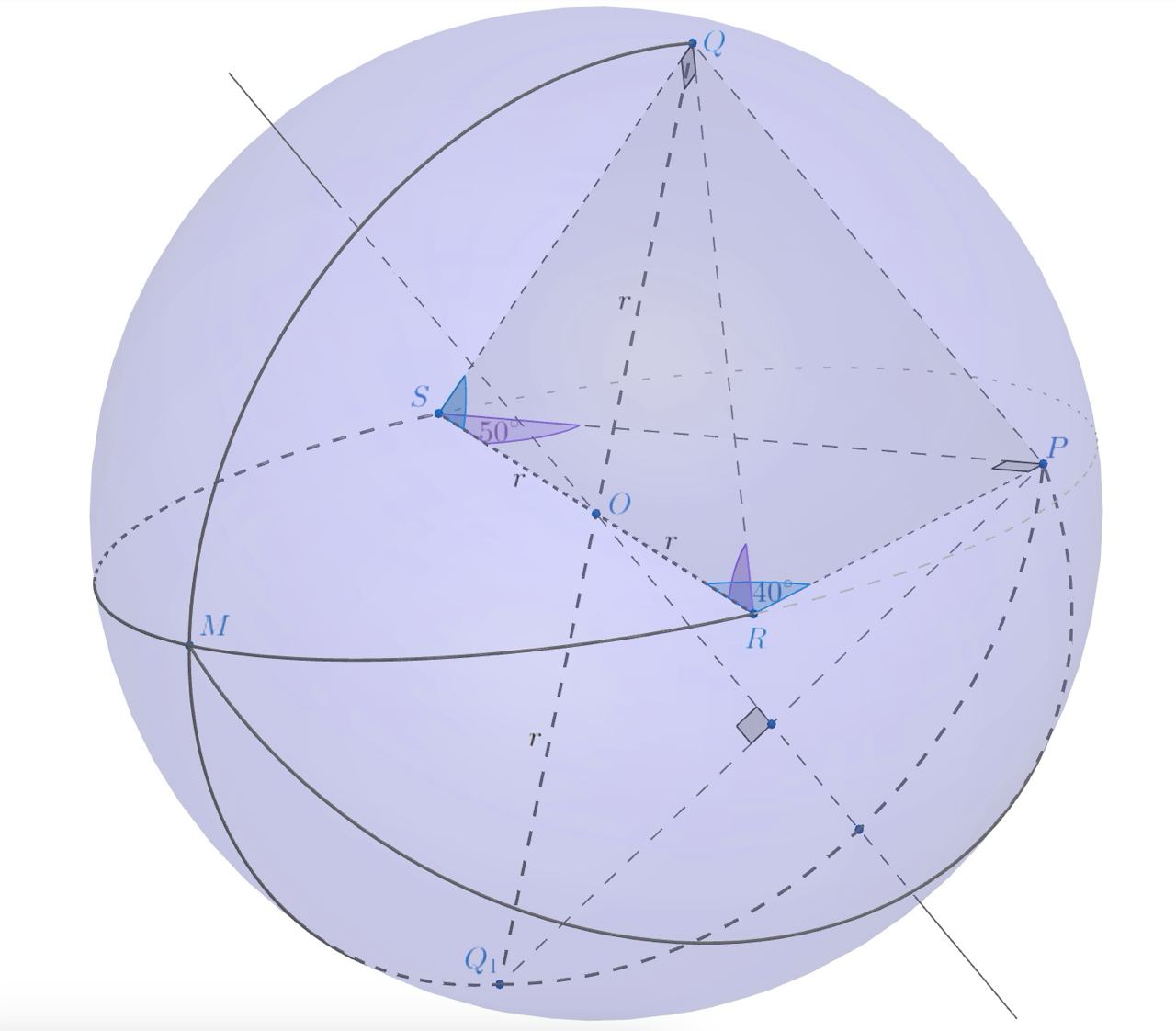
Так как
то треугольники и
— прямоугольные с общей гипотенузой
. Если
— середина отрезка
, то по свойству медианы
прямоугольного треугольника
. Следовательно, радиус описанной сферы равен 3, а точка
— её
центр.
Обозначим через сферическое расстояние между точками
и
. По условию задачи необходимо найти площадь множества
на сфере, состоящего в точности из точек
, для которых
Поскольку — диаметр сферы, то точки
и
лежат на одной окружности большого круга; следовательно,
Неравенство (1) перепишется в виде
Пусть — точка, симметричная точке
относительно центра сферы
. Так как
и
— концы диаметра сферы,
то
Подставляя в неравенство (2), получаем
Так как , то
не является диаметром, а потому
. Итак,
есть множество точек на сфере, сферическое
расстояние от которых до одной точки на сфере не превосходит сферического расстояни до другой точки на сфере. В силу симметрии
(относительно плоскости, проходящей через центр сферы перпендикулярно отрезку
,
— половина сферы и её площадь
равна
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




