Стереометрия на ОММО
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде с рёбрами
и
проведены два сечения – плоскостью,
проходящей через диагональ
, и плоскостью, проходящей через диагональ
. Найдите наибольшее возможное значение суммы
площадей поверхностей многогранников, на которые эти сечения разбивают данный параллелепипед.
Источники:
Подсказка 1
Нарисуйте картинку и попробуйте понять: что точно, вне зависимости от положения сечений будет содержаться в искомой сумме? Можем ли мы как-то избежать попадания в эту сумму какой-то части исходного параллелепипеда? А сколько раз туда попадут части наших сечений?
Подсказка 2
Итак, получается, что как бы ни были расположены сечения, их площади дважды войдут в искомые площади поверхностей. Значит надо эти площади максимизировать!
Подсказка 3
Какой фигурой будет являться каждое сечение? Как площади сечений связаны с длинами диагоналей? Исследуйте, где должны быть расположены вершины параллелограмма-сечения, чтобы расстояние до диагонали параллелепипеда было наибольшим.
Подсказка 4
Осталось лишь посчитать все нужные длины, призвав на помощь теорему Пифагора. Будьте внимательны к арифметике и задача окажется убита!
Сумма площадей поверхностей многогранников, на которые разбивается параллелепипед сечениями, равна сумме площади поверхности параллелепипеда и площадей внутренних поверхностей. Сумма площадей внутренних поверхностей равна удвоенной сумме площадей сечений.
Найдем наибольшую возможную площадь сечения, проходящего через диагональ произвольного параллелепипеда с
ребрами
. Сечением является параллелограмм
, вершины которого лежат на противоположных рёбрах
параллелепипеда. Площадь параллелограмма равна произведению длины диагонали
на расстояние от точки
до
.

Рассмотрим проекцию параллелепипеда на плоскость, перпендикулярную диагонали . На рисунке видно, что расстояние от точки
ломаной
до точки
, то есть до диагонали
, наибольшее, если
совпадает с одной из вершин
или
.
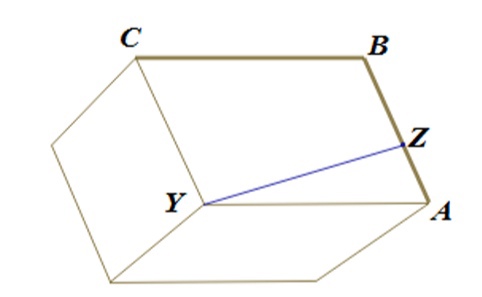
Значит, сечение проходит через одно из ребер параллелепипеда. Таким образом, наибольшую площадь имеет одно из диагональных сечений. Все эти сечения являются прямоугольниками. Найдем наибольшую из их площадей
Из условия следует, что,
, и
. Поэтому
и
. Значит,
наибольшую площадь имеет сечение, проходящее через наибольшее ребро. По условию наибольшую длину имеет ребро
, значит,
наибольшую площадь
имеют сечения
и
.
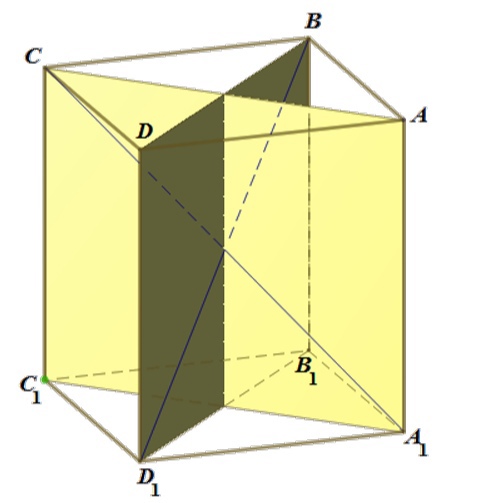
Сумма площадей поверхностей многогранников, на которые разбивается параллелепипед этими сечениями (см. рисунок), равна
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




