Прямая Эйлера

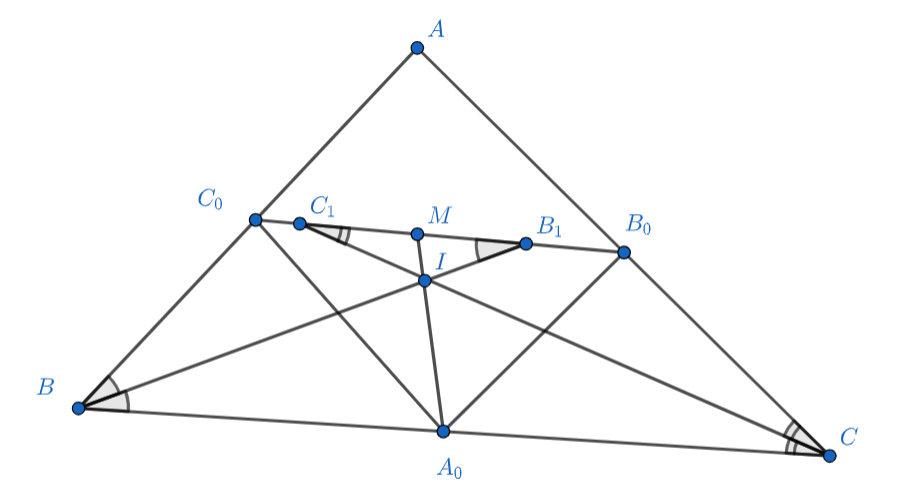
Первое решение.

Пусть и при этом Пересечём биссектрисы и с в точках и соответственно. Тогда в силу параллельности равны отмеченные углы и Отсюда следует, что обе точки лежат на отрезке Кроме того, и тогда Пусть тогда в силу подобия Осталось заметить, что что и требовалось. Другие соотношения длин сторон рассматриваются аналогично, поменяется только порядок точек на прямой

Второе решение.

Ясно, что исходный треугольник можно перевести гомотетий в серединный треугольник Центром этой гомотетии (неподвижной точкой) является точка пересечения медиан треугольника ведь медианы серединного треугольника пересекаются тоже в точке Коэффициент этой гомотетии равен то есть сначала надо стороны треугольника уменьшить в два раза, а потом сделать центральную симметрию относительно Куда перейдёт точка при этой гомотетии? С одной стороны, в центр вписанной в серединный треугольник окружности. С другой стороны, по определению это будет такая точка на прямой , что Получаем, что на прямой Нагеля для серединного треугольника нашлась такая точка что Значит, для серединного треугольника точка является точкой Нагеля, а прямая — нагелианой. Известно, что нагелиана делит периметр треугольника пополам, потому что отрезок касательной к вневписанной окружности как раз равен разности полупериметра треугольника и прилежащей стороны.