Прямая Эйлера
Ошибка.
Попробуйте повторить позже
Центр вписанной окружности треугольника
лежит на его прямой Эйлера. Докажите, что треугольник
—
равнобедренный.
Подсказка 1
У нас есть центр описанной окружности, значит, мы явным образом можем определить серединный перпендикуляр (высота из точки О на сторону). Также у нас есть центр вписанной окружности, а значит, мы можем в явном виде построить биссектрису (провести через вершину и инцентр прямую). А какая связь у нас есть между серединным перпендикуляром и биссектрисой? Как ее использовать здесь?
Подсказка 2
Действительно, серединный перпендикуляр и биссектриса пересекаются на описанной окружности. А если опустить еще и высоту к той же стороне? Как теперь использовать параллельность серединного перпендикуляра и высоты? А как к этому добавить условие про то, что I лежит на прямой OH?
Подсказка 3
Верно, в силу того, что I лежит на OH, и высота и серединный перпендикуляр параллельны, следует равенство HI/IO=AH/OA1(A1-точка пересечения биссектрисы и серединного перпендикуляра к BC, на дуге не содержащей точку А). Но ведь ничего не мешает записать нам такое же отношение, но для другой стороны(то есть, сделать такие же построения как сделали для стороны BC и записать для соответственных сторон). Что можно заметить?
Подсказка 4
Если B1-точка пересечения серединного перпендикуляра к АС и описанной вокруг АВС окружности, на дуге не содержащей точку В, то выходит, что OI/IH=OB₁/BH. Значит OB₁/BH=OA₁/AH. При этом OB₁=OA₁, так как это радиусы. Значит, AH=BH. Осталось только доказать, что если так, то AC=BC.
Продлим прямые и
до пересечения с описанной окружностью, обозначим точки пересечения соответственно как
и
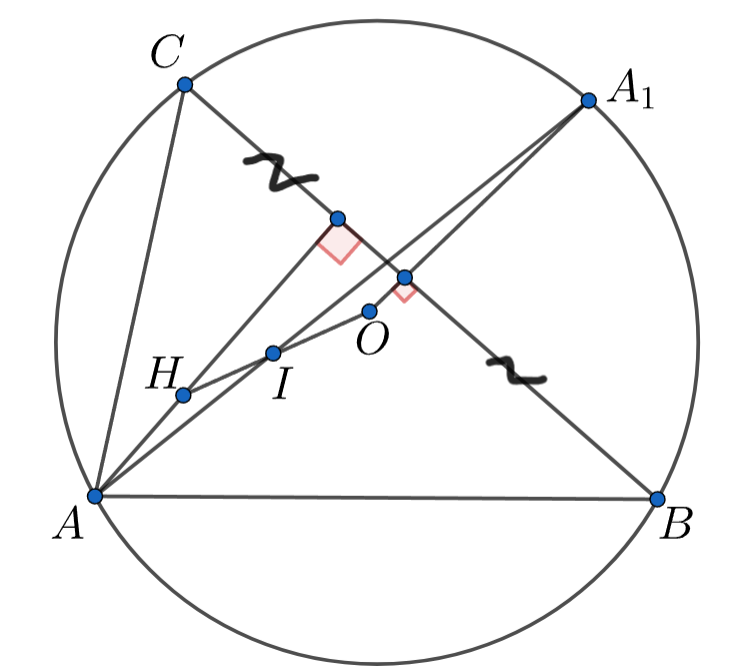
Заметим, что — серединный перпендикуляр к
откуда вытекает параллельность
Из неё, в свою очередь, следует,
что
Аналогично можно получить
Но как радиусы описанной окружности, так что
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




