Главная
Каталог задач
Каталог заданий по ЕГЭ - Математика
Длина окружности или дуги и площадь круга или сектора

Тема 1. Геометрия на плоскости (планиметрия)

1.19 Длина окружности или дуги и площадь круга или сектора

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела геометрия на плоскости (планиметрия)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#77

Длина окружности с центром в точке $O$ равна 12. $∠AOB = 120∘,$ точки $A$ и $B$ лежат на окружности и разбивают её на две дуги. Во сколько раз длина большей из получившихся дуг превосходит длину меньшей?

$PIC$

Показать ответ и решение

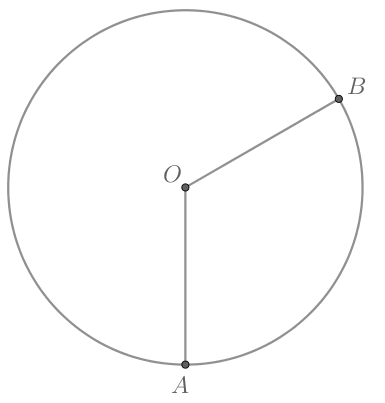
Длины дуг относятся так же, как их градусные меры. Так как $O$ — центр окружности, то $∠AOB$ — центральный.

Градусная мера дуги, меньшей, чем полуокружность, есть градусная мера центрального угла, который на неё опирается. Тогда градусная мера меньшей из дуг равна $120∘,$ а большей из дуг $240∘.$

Градусная мера большей дуги в $240 :120 = 2$ раза больше, чем градусная мера меньшей дуги.

Ответ: 2

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#542

На рисунке изображены две окружности с общим центром $O,$ где радиусы $OB = 3$ и $OA = 1,$ а угол $∠BOD = 90∘.$ Найдите площадь фигуры $ABCDEF A$ деленную на $π.$

$PIC$

Показать ответ и решение

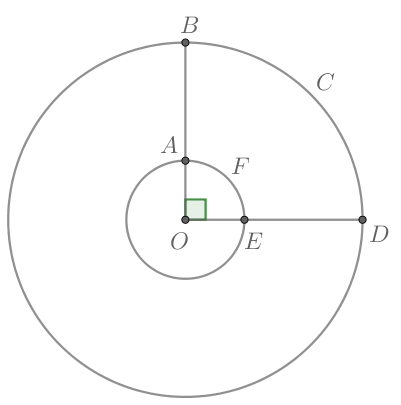
Площадь сектора с углом $90∘$ в большой окружности равна

2 Sбол. = π⋅3∘ ⋅90∘ = 9π 360 4

Площадь сектора с углом $90∘$ в маленькой окружности равна

π ⋅12 ∘ π Sмал. = 360∘-⋅90 = 4

Тогда

SABCDEFA-= Sбол.−-Sмал.= 2 π π

Ответ: 2

Ошибка.
Попробуйте повторить позже

Задача 3#543

Длины дуг окружности с центром $O$ отмечены на рисунке.

$PIC$

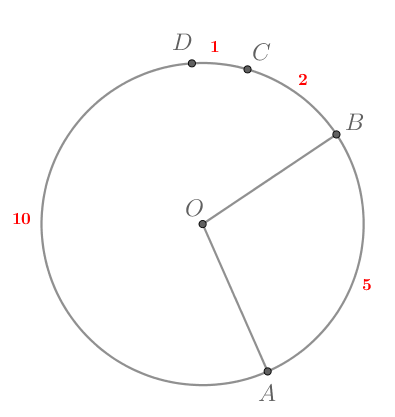
Найдите $∠AOB.$

Показать ответ и решение

Длина всей окружности складывается из длин составляющих ее дуг

C = 1 +2 +5 +10 =18

Тогда

C∠ACOB-= ∠A3O6B0∘- ⇒ 158 = ∠A3O6B0∘-- ⇒ ∘ ⇒ ∠AOB = 100

Ответ: 100

Ошибка.
Попробуйте повторить позже

Задача 4#544

$PIC$

Точки $O1$ и $O2$ — центры окружностей, изображенных на рисунке. Найдите площадь закрашенной фигуры $AO1BCO2DEA,$ если $AO1 = √2-. π$

Показать ответ и решение

Из рисунка видно, что

AO2 = 2 ⋅AO1 = √4-- π

Закрашенную фигуру разобьем на две фигуры: $AO2DEA$ и $O1BCO2O1.$ Первая является половиной круга радиуса $AO2,$ а вторая является сектором круга радиуса $AO1,$ который задан углом $90∘.$ Тогда площадь закрашенной фигуры можно найти как сумму площадей составляющих ее фигур:

( 4√-)2 (√2)2 SAO BCO DEA = π-⋅--π--+ π-⋅--π-- = 9 1 2 2 4

Ответ: 9

Ошибка.
Попробуйте повторить позже

Задача 5#558

Длина окружности с центром в точке $O$ равна 18 см. Площадь сектора $AOB$ равна $18 π$ см $2 .$ Найдите длину дуги $AB$ этого сектора. Ответ дайте в сантиметрах.

$PIC$

Показать ответ и решение

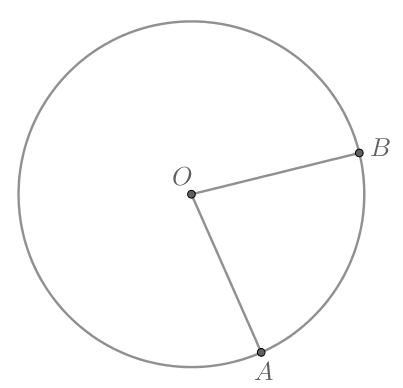
Длина окружности равна $2πR,$ где $R$ — радиус этой окружности. Для данной окружности $2πR =18$ см, тогда $9- R = π$ см.

Площадь сектора, градусная мера дуги которого есть $α$ равна $πR2 ⋅-α-. 360$

Длина дуги с градусной мерой $α$ равна $α 2πR ⋅360.$

Из этих формул видно, что длина дуги с градусной мерой $α$ получится из площади сектора, градусная мера дуги которого есть $α,$ при помощи умножения этой площади на $2-. R$

Длина дуги $AB$ данного сектора равна

18 2π -π ⋅9-= 4 см

Ответ: 4

Ошибка.
Попробуйте повторить позже

Задача 6#1173

Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны $-4- √π$ и $-2-- √ π.$

$PIC$

Показать ответ и решение

Для того, чтобы найти площадь кольца, нужно из площади большего круга вычесть площадь меньшего круга:

( )2 ( )2 ( ) S = π ⋅ √4- − π ⋅ √2- = π ⋅ 16− 4- = 12 π π π π

Ответ: 12

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#1422

Внутри большой окружности расположена маленькая, радиус которой в 2,5 раза меньше, чем радиус большой окружности. Найдите отношение площади зеленой области $U$ к площади круга, ограниченного большой окружностью.

$PIC$

Показать ответ и решение

Обозначим радиус меньшей из окружностей за $r,$ тогда радиус большей окружности $2,5⋅r.$

Площадь круга, ограниченного окружностью радиуса $R,$ равна $πR2.$

Площадь меньшего круга равна $πr2,$ а площадь большего равна

2 2 π⋅(2,5r) = 6,25πr

Площадь области $U$ равна разности площадей большего и меньшего кругов и равна

2 2 2 6,25πr − πr =5,25πr

Искомое отношение площадей есть

2 5,25πr2-= 0,84 6,25πr

Ответ: 0,84

Ошибка.
Попробуйте повторить позже

Задача 8#1844

Две окружности касаются внутренним образом так, что один из радиусов большей окружности совпадает с диаметром меньшей окружности (смотри рисунок). Найдите радиус большей окружности, если площадь зеленой области равна $48π.$

$PIC$

Показать ответ и решение

Обозначим за $R$ – радиус большей окружности и одновременно диаметр меньшей. Тогда площадь зеленой области $S$ можно выразить через площади кругов следующим образом:

2 S = πR2− πR--= 3πR2 4 4

Тогда

3 2 S = 48π ⇒ 4πR = 48π ⇒ ⇒ R2 = 64 ⇒ R =8

Ответ: 8

Ошибка.
Попробуйте повторить позже

Задача 9#2725

Две равные окружности пересекаются так, как показано на рисунке. Найдите длину внешней границы полученной фигуры, если длина окружности равна $12.$

$PIC$

Показать ответ и решение

$PIC$

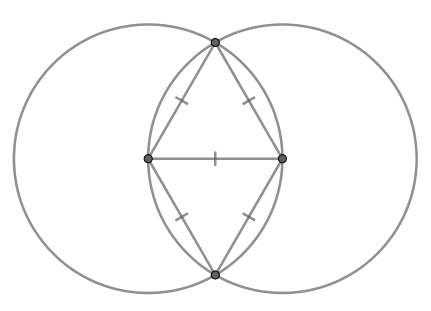
Соединим центры окружностей друг с другом, а также центр каждой окружности с точками пересечения окружностей друг с другом. Можно выделить два равносторонних треугольника, стороны которых равны радиусам окружностей. Дуга одной из окружностей, расположенная во внутренней области образовавшейся фигуры, опирается на угол равный двум углам равностороннего треугольника, то есть на угол равный $120∘,$ а значит ее длину можно найти из следующего соотношения: