Планиметрия на Физтехе
Ошибка.
Попробуйте повторить позже
B прямоугольный треугольник вписана окружность
с центром
которая касается сторон
и
в точках
и
соответственно. Прямая, проходящая через точку
пересекает стороны
и
в точках
и
соответственно. Найдите
радиус окружности
если
Найдите
если дополнительно известно, что прямая
параллельна
Источники:
Подсказка 1
На рисунке есть очень много прямых углов, давайте их все отметим и попробуем найти какие-то равные отрезочки
Подсказка 2
Так как в четырёхугольнике KILB три прямых угла и две равные смежные стороны, KILB – квадрат! Обозначим его сторону за r (ведь это фактически радиус вписанной окружности), можно ли теперь записать какое-то уравнение, чтобы найти эту неизвестную?
Подсказка 3
Так как KI || BN, △KMI ∼ △BMN, записав отношение их подобия, находим r) Теперь нужно как-то найти АС, сразу в глаза бросаются подобные треугольники АВС и MBN, если мы найдём коэффициент их подобия, то сможем найти АС, ведь MN легко вычислить по теореме Пифагора!
Подсказка 4
Давайте опустим высоты ВН и ВВ₁ треугольников BMN и АВС соответственно, знаем ли мы НВ₁?
Подсказка 5
НВ₁ – это расстояние между прямыми MN и АС, то есть расстояние от точки I до АС, что, разумеется, равно радиусу вписанной окружности! Тогда нам остается посчитать, чему равны ВН, MN и ВВ₁ = ВН + НВ₁, и найти АС через коэффициент подобия)
Пусть радиус окружности Г равен
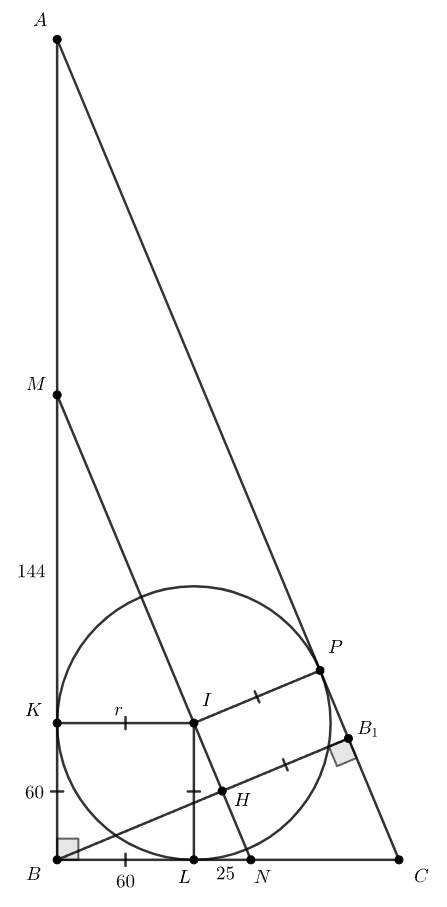
Заметим, что так как
касается окружности Г в точке
Аналогично,
Также заметим, что
как
радиусы Г. Получается, в четырехугольнике
две смежные стороны равны и три угла являются прямыми, откуда этот
четырёхугольник — квадрат, то есть
Два прямоугольных треугольника и
подобны, так имеют общий угол
Отсюда
Получается,
______________________________________________________________________________________________________________________________________________________
Замечание: Мы пользуемся тем, что точка лежит на отрезке
так как если бы она лежала на
то прямая
пересекала бы продолжение стороны
а не саму сторону, что противоречило бы условию. Аналогично точка
лежит на
______________________________________________________________________________________________________________________________________________________
Таким образом, а
По теореме Пифагора
Пусть окружность Г касается в точке
Тогда
и
Отсюда расстояние между параллельными прямыми
и
равно 60.
Проведём — высоту треугольника
Пусть
Из параллельности
и
имеем, что
то есть
— высота треугольника
Из формул площадей прямоугольного треугольнька можно выразить, что длина высоты — это
произведение катетов делить на гипотенузу, то есть
При этом — это какое-то рассояние между параллельными прямыми
и
то есть
а
Прямоугольные треугольники и
подобны, так как
откуда
Итак,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




