Стереометрия на Физтехе

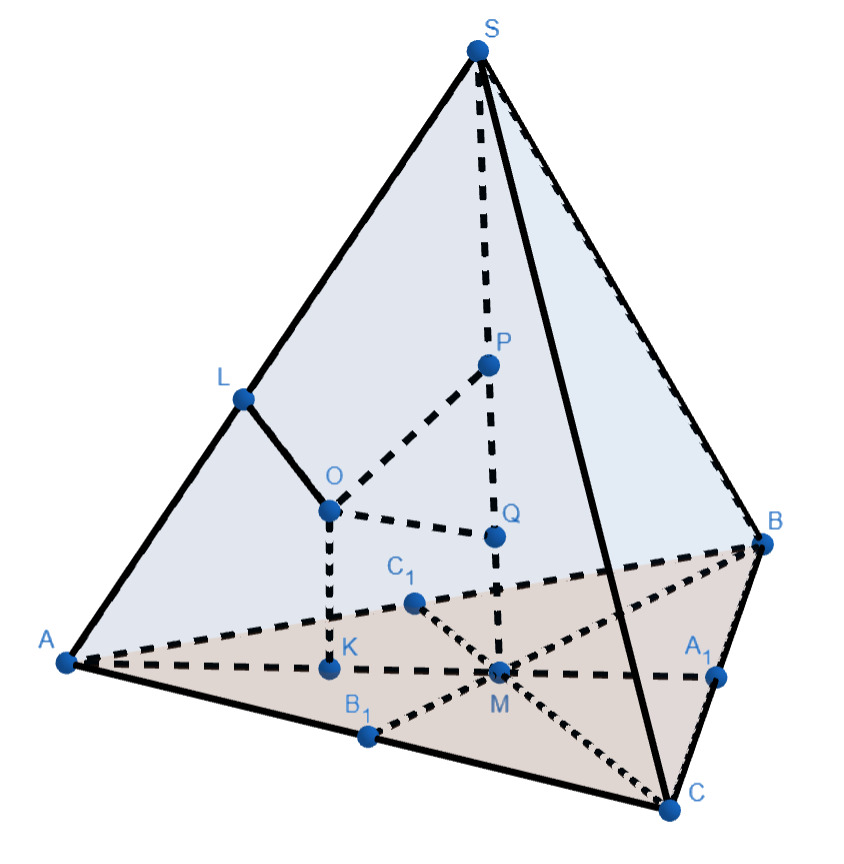
За будем обозначать плоскость, проходящую через точки , и

Возьмем на прямой такую точку , что . Тогда

На прямой же возьмём точку такую, что . Получается, что плоскость Тогда лежит в плоскости . пересекает плоскость основания по прямой (), параллельной

Пусть . Тогда , . Треугольник будет правильным (есть 2 угла по ), т.е. .

т.к. это 2 угла с параллельными сторонами.

Рассматриваем треугольник . . Подставляем найденные значения.

Минимум выражения слева достигается при и равно . Тогда

Если бы призма была прямая, то площади боковых граней были бы равны. Значит, призма наклонная.

Обозначим призму площади из условия

Пусть — высоты параллелограммов и Тогда т.к. площади равны, а также равны их основания, так как равносторонний треугольник.

Пусть — проекция на плоскость Тогда следовательно, точка равноудалена от прямых и

(a) Рассмотрим случай, когда принадлежит биссектрисе угла — высота, медиана и биссектриса в равностороннем треугольнике.

Тогда получаем, что — прямоугольник. Пусть сторона треугольника равна Посчитаем площадь прямоугольника и параллелограмма.

Но тогда

получаем противоречие.

(b) Рассмотрим случай, когда принадлежит внешней биссектрисе угла

Но следовательно, откуда следует, что высота параллелограмма совпадает с высотой призмы В итоге

а)

Поскольку — касательная к сфере а и — секущие к ней, то по теореме о касательной и секущей

Аналогично,

А поскольку то

В итоге получаем

Так как как касательные к сфере проведённые из точки то

А поскольку медианы треугольника точкой пересечения делятся в отношении считая от вершины, то

Кроме того,

При этом

то есть

Отсюда прямоугольный и Далее имеем

Значит,

б)

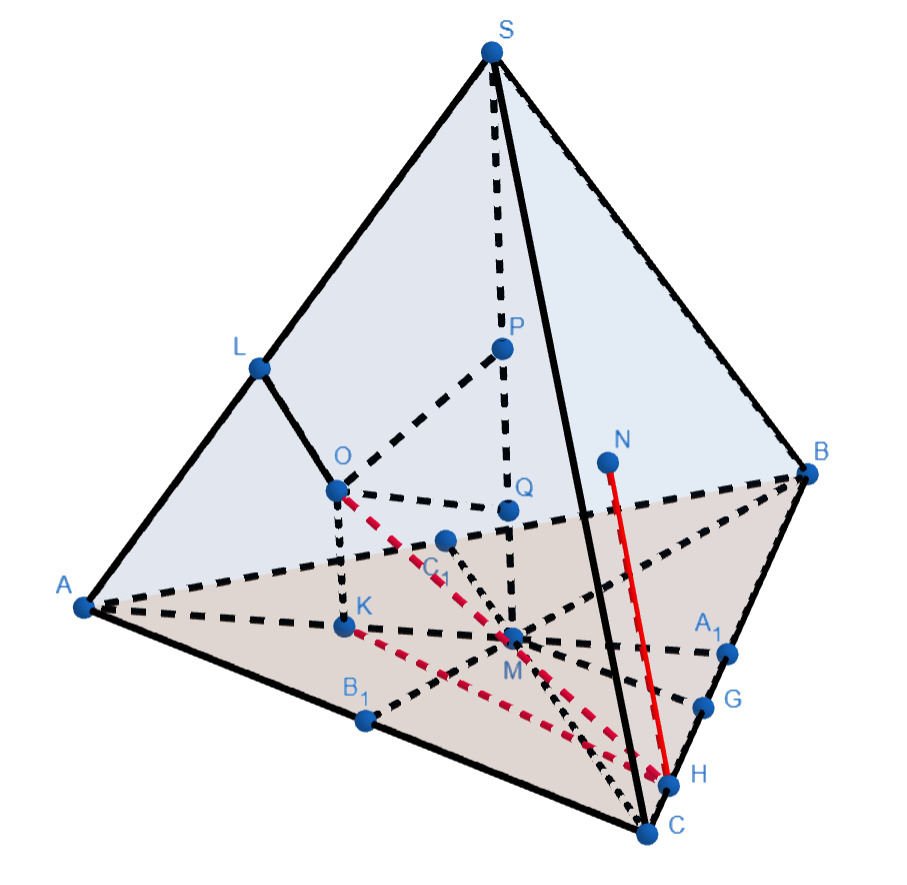
Пусть и — проекции точек и на прямую соответственно. Заметим, что потому что и — точки касания сферы со сторонами двугранного угла пирамиды при ребре Поэтому искомый угол равен

где — центр сферы

Далее имеем

Так как как касательные к то

Отсюда получаем

Из подобия и имеем

Окончательно,

Пусть - середины рёбер соответственно. Из теоремы о средней линии треугольника следует, что и - параллелограммы. Они вписаны в окружности, являющиеся сечениями сферы плоскостями и , поэтому эти параллелограммы - прямоугольники. Угол — прямой; прямые и перпендикулярны, так как

Отметим в плоскости точку такую, что а точки и лежат по разные стороны от прямой (треугольник может быть получен из треугольника поворотом вокруг прямой

Из равенства треугольников и следует, что основания их высот, опущенных на — это одна и та же точка (назовём её Плоскость перпендикулярна (так как поэтому Поскольку и то плоскость перпендикулярна и

Значит, диагонали четырёхугольника пересекаются под прямым углом (в точке ). По теореме Пифагора

Следовательно,

Из прямоугольного треугольника находим

Радиус сферы, описанной около пирамиды , не меньше радиуса окружности, описанной около грани . Пирамида, для которой достигается равенство, существует. Докажем это.

Рассмотрим сферу радиуса и окружность - её сечение, проходящее через центр сферы. В сечении сферы указанной плоскостью получится окружность с диаметром , в которую можно вписать прямоугольный треугольник . По теореме косинусов из треугольника находим, что

По теореме синусов

Пусть — середина и — медианы равнобедренных треугольников и , a значит, биссектрисы и высоты. То есть . Значит, отрезок перпендикулярен плоскости , следовательно, .

Таким образом, лежит в плоскости, перпендикулярной оси цилиндра (обозначим эту плоскость через ). Сечение цилиндра этой плоскостью — окружность, а является хордой этой окружности. Тогда радиус цилиндра минимален, если диаметр. Отметим, что это возможно в силу того, что отрезки и длиннее, чем . Действительно, из треугольников и следует, что

Рассмотрим тетраэдр, в котором является диаметром цилиндра. Возможны 2 случая: точки и лежат по одну (этот случай представлен выше) или по разные стороны плоскости .

Пусть - проекция точек и на плоскость . Угол , так как он вписан в окружность и опирается на её диаметр. в силу равенства треугольников и . Тогда . По теореме Пифагора в прямоугольных треугольниках и соответственно: .

Тогда, если точки и лежат по одну сторону от плоскости , то . Если точки и лежат по разные стороны от плоскости , то .

Доказано, что 𝐴𝐵 – диаметр цилиндра наименьшего радиуса – 2 балла; если при этом не проверено, что точки 𝐶 и 𝐷 могут лежать на боковой поверхности такого цилиндра (например, можно доказать, что треугольники 𝐴𝐵𝐶 и 𝐴𝐵𝐷 остроугольные; можно сделать, как в решении), то 1 балл вместо 2;

найдены оба значения 𝐶𝐷 – 3 балла;

найдено только одно значение 𝐶𝐷 – 1 балл вместо 3.

Обозначим точки пересечения прямой со сферой через и (точка лежит на отрезке , а — вне него). Пусть радиус сферы равен . Треугольники и прямоугольные (углы при вершинах прямые, так как касательные перпендикулярны радиусам, проведённым в точку касания). Эти треугольники равны по катету и гипотенузе — общая), следовательно, пусть . Высоты, опущенные из точек на гипотенузу , paвны, а их основания — одна и та же точка , лежащая в плоскости (назовём эту плоскость . Пусть и касательные плоскости к сфере, проходящие через точки и , а и — точки пересечения этих плоскостей с прямой . По условию площади сечений трёхгранного угла этими плоскостями равны соответственно и . Рассмотрим сечение трехгранного угла и сферы плоскостью (см. рис. и обозначения на нем). Так как и , то . Тогда сечения трёхгранного угла плоскостями и — подобные треугольники, плоскости которых параллельны (все они перпендикулярны .

Если — площадь треугольника, получающегося в сечении трёхгранного угла плоскостью , то из подобия Следовательно, Тогда откуда a Отсюда

Далее, Значит, откуда

а) Пусть радиус сферы равен . Обозначим точки пересечения прямой со сферой через и (точка лежит на отрезке , а — вне него). Треугольники и прямоугольные (углы при вершинах прямые, так как касательные перпендикулярны радиусам, проведённым в точку касания). Эти треугольники равны по катету и гипотенузе — общая), следовательно, (обозначим эти углы через ); высоты, опущенные из точек на гипотенузу , равны, а их основания — одна и та же точка , лежащая в плоскости (назовём эту плоскость . Пусть — касательная плоскость к сфере, проведённая через точку . Обозначим точку пересечения и через . Рассмотрим сечение пирамиды и сферы плоскостью

Из прямоугольного треугольника получаем . Тогда

Пусть площадь сечения пирамиды плоскостью равна , а плоскостью . Из подобия следует, что

Следовательно,

б) Если плоскости и параллельны, то точка совпадает с точкой такой, что

Тогда, обозначив площадь треугольника через , получаем

Противоположные стороны четырёхугольника попарно равны, так что он параллелограмм. Поскольку плоскость пересекает плоскости и по параллельным прямым и , эти прямые параллельны прямой пересечения этих плоскостей, то есть . Аналогично, . В правильной треугольной пирамиде скрещивающиеся рёбра перпендикулярны друг другу, поэтому , а прямоугольник. Следовательно, радиусы окружностей и равны

Отсюда также следует, что прямоугольник симметричен относительно плоскости , содержащей ребро и середину . Тогда и конусы и также симметричны относительно этой плоскости. Поэтому — середина .

Обозначим через и середины сторон и соответственно, а через и центры окружностей и соответственно; эти четыре точки лежат на оси симметрии прямоугольника , параллельной , а значит — в плоскости . Более того, , то есть треугольники и подобны.

Пусть . Тогда . Поскольку , из подобия получаем

Аналогично,

C другой стороны, так как конус прямой, имеем , причём . Отсюда

Итак, , и из подобия имеем

откуда и . Пусть пересекает в точке . Тогда — высота треугольника , причём (поскольку ) . Значит, . Поскольку — прямоугольник, так что . Отсюда .

Отметим точку в качестве вершины пирамиды, точку в качестве центра , точку в качестве центра описанной окружности треугольника и в качестве середины . Так как равносторонний, то это еще и центр пересечения медиан, а значит, проходит через и и . Так как проходит через вершины треугольника и касается отрезка в точке , то и . Мы знаем, что и поэтому . Получается, что мы знаем, что точка лежит на плоскости , проходящей через и параллельной , и лежит на прямой , перпендикулярной и проходящей через . Значит, либо принадлежит , но тогда перпендикулярна двум разным прямым параллельным ( и ) и тогда все три стороны перпендикулярны основанию, а такого не бывает, либо и пересекаются в одной точке и . Тогда и (по формуле для равностороннего треугольника).

Спроецируем точки и на плоскость . Тогда так как проекция на это , то и поэтому . Также можно заметить .

Прямоугольные треугольники и равны по катету и гипотенузе, поэтому . Значит, высота в равнобедренном треугольнике равна , так как середина и равна . Тогда

Значит, . Тогда

Пусть — проекция на . Тогда и . С другой стороны, поскольку , то . Отсюда .

Воспользуемся формулой радиуса вписанной сферы , где — объём, а — площадь поверхности пирамиды. Объёмы пирамид и равны (грань общая, а вершины и равноудалены от плоскости ); кроме того и (медиана делит площадь треугольника пополам). Значит, равенство сфер, вписанных в пирамиды и , эквивалентно условию или равенству высот, проведённых к стороне в треугольниках и .

Пусть высота пирамиды, а высота в треугольнике . Объём пирамиды равен , а её высота из вершины равна 3, то есть . Значит, площадь основания пирамиды равна . Тогда сторона основания , а высота треугольника равна 5. Значит, также равно 5. Из прямоугольного треугольника находим , т.е. точка находится на расстоянии 4 от прямой ( лежит на одной из двух прямых, параллельных , на расстоянии 4 от неё). Тем самым, угол между гранями при ребре равен .

Из условия, что грани и взаимно перпендикулярны, следует, что лежит на . Так как , то . Значит или . Тогда или .

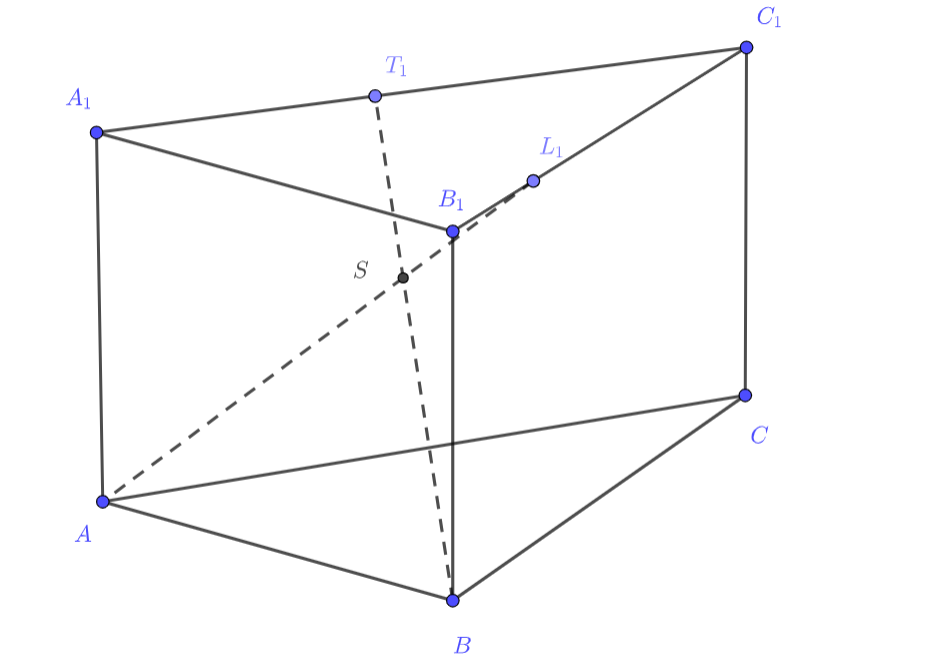
(a) Точки и лежат на окружности с диаметром значит, (т.е. и высоты треугольника Прямая — это проекция прямой на плоскость основания, при этом Тогда по теореме о трёх перпендикулярах т.e.

(b) Поскольку прямые и пересекаются, то все четыре точки и лежат в одной плоскости (назовём её ). Значит, прямые и лежат в одной плоскости а так как они не пересекаются (поскольку лежат в параллельных друг другу основаниях призмы), то Значит, Трапеция вписана в окружность, следовательно, она равнобокая, тогда углы при её основании равны, и поэтому треугольник равнобедренный

Треугольники и подобны по двум углам. Из равенства треугольников и следует, что поэтому оба треугольника и равнобедренные с основаниями и соответственно. Значит, откуда

(c) Если то ; . Значит, площадь основания призмы равна объём призмы равен .

(a) Из соображений симметрии (относительно плоскости ) плоскость проходит через точку — и, значит, через центр грани . Отрезки и — проекции параллельных отрезков и на прямую , причём . Значит, .

(b) Поскольку сфера касается всех боковых граней призмы, её проекция на основание есть окружность, вписанная в это основание. Значит, . Кроме того, и — это две параллельные плоскости, касающиеся сферы, поэтому расстояние между ними равно диаметру сферы, то есть 6. Так как , этим расстоянием является отрезок , поэтому .

Обозначим . Поскольку — высота прямоугольного треугольника , то

и, следовательно, . Тогда

и

Получаем уравнение

поскольку .

Наконец, высота призмы равна

А объём призмы равен

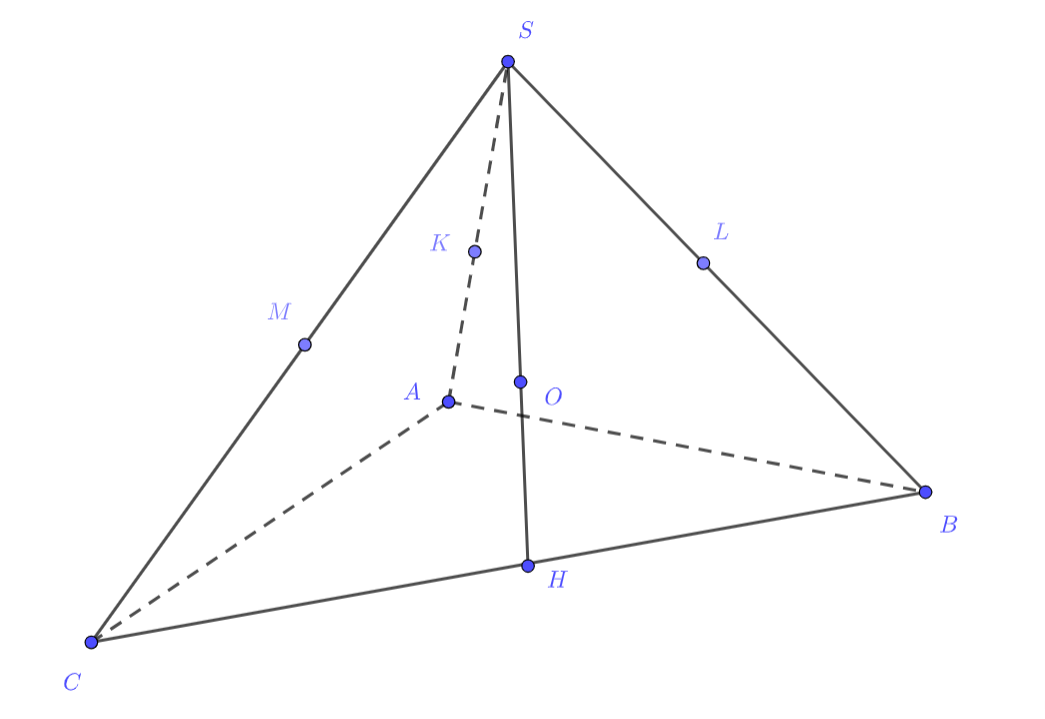
Пусть — центр сферы — основания перпендикуляров, опущенных из точки на ребра соответственно; — высота пирамиды и — радиусы сфер и соответственно.

a) Поскольку точка лежит на серединном перпендикуляре к отрезку она равноудалена от концов этого отрезка, т.е. Аналогично и Значит, поэтому точка является центром сферы . Следовательно, расстояние между центрами сфер равно нулю.

b) Из равенства прямоугольных треугольников , и — общая сторона) следует, что Поскольку точки — это середины боковых рёбер пирамиды, отсюда получаем, что боковые рёбра равны между собой. Тогда высота пирамиды проходит через центр окружности, описанной около основания (действительно, по катету и гипотенузе, откуда ). Но в пирамиде боковые рёбра также равны между собой как радиусы сферы ; значит, и её высота, проведённая из вершины проходит через центр окружности, описанной около основания. Таким образом, высота пирамиды проходит через точку Кроме того, точка является центром окружности, описанной около основания. Поскольку треугольник прямоугольный, — это середина гипотенузы Так как отрезок перпендикулярен плоскости основания, он равен радиусу сферы

Для нахождения соотношения между радиусами рассмотрим прямоугольный треугольник Точка — середина гипотенузы на катете находится точка причём , Треугольники , и равны по катету и гипотенузе, следовательно, Значит, Тогда из треугольника находим, что

c) поэтому треугольник — равносторонний, B равнобедренном треугольнике известны боковые стороны и угол при основании Отсюда находим, что . По теореме Пифагора для треугольника находим, что поэтому объём пирамиды равен

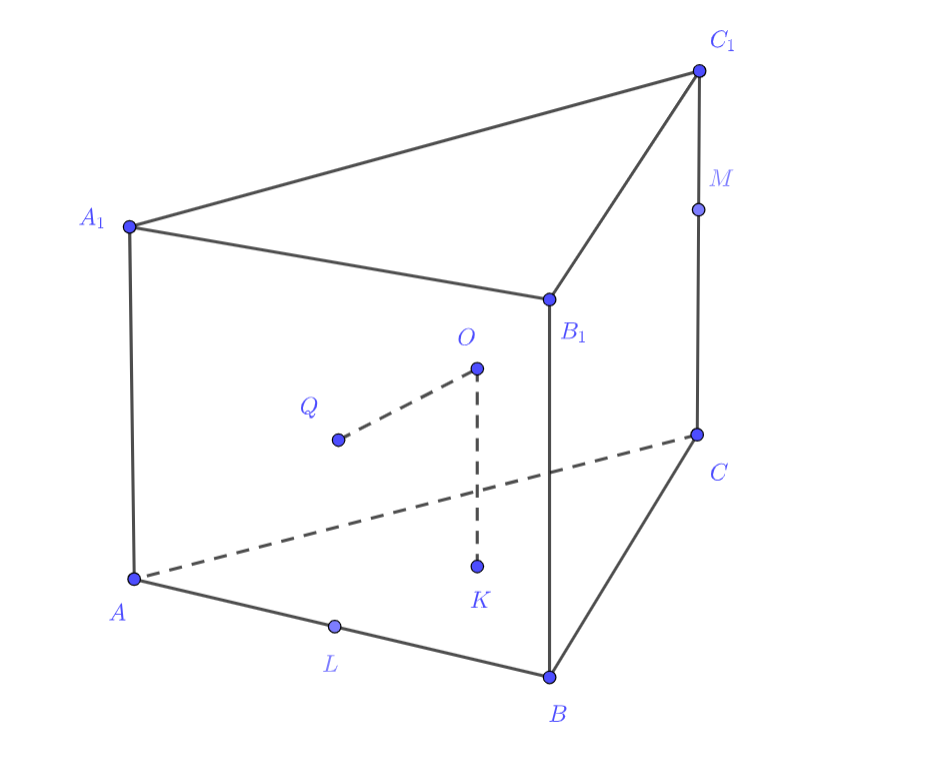
Введём обозначения: — центр грани середина ребра — центр сферы, описанной около пирамиды (т.е. — центр грани ); — центр сферы, описанной около пирамиды .

(a)  3начит, объём пирамиды составляет две трети объёма призмы.

(b) Сторона равностороннего треугольника равна , следовательно, , как радиус описанной окружности.

Рассмотрим прямоугольную трапецию . В ней известны стороны и диагональ По теореме Пифагора из треугольника находим, что Опустим из точки перпендикуляр на отрезок . Тогда

(c) Обозначим Тогда

Отрезки и равны как радиусы сферы. Решая получающееся уравнение, находим, что Тогда площадь поверхности призмы

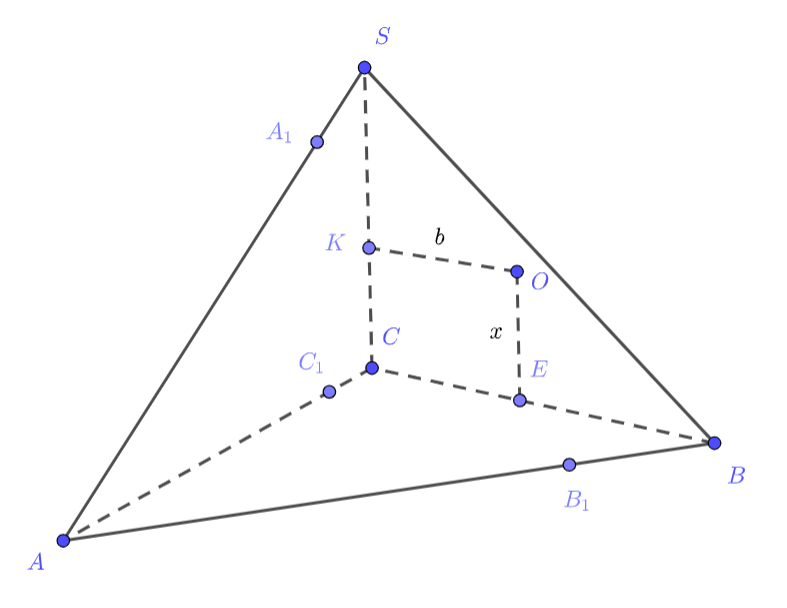
Обозначим Пусть и проекции точки на прямые и соответственно. Пусть — радиус сферы.

Так как — перпендикуляр к плоскости , а то по теореме о трёх перпендикулярах получаем . Аналогично Из равенства прямоугольных треугольников и следует, что Из равенства прямоугольных треугольников и так как получаем, что Тогда Кроме того, из равенств отрезков касательных, проведённых к сфере из точки следует, что Для нахождения и выразим из треугольников и Так как и то где Следовательно, откуда получаем

T. e. Тогда .

Имеем . Пусть . Тогда

Пусть плоскость П пересекается с прямыми и в точках и соответственно.

В плоскости из прямоугольного имеем

Далее из прямоугольного имеем

В плоскости из прямоугольного имеем

Так как перпендикулярно плоскости , то углом между прямой и плоскостью является

Так как

то расстояние от точки до плоскости равно

В плоскости из по теореме косинусов находим

Рассмотрим . Пусть . Тогда по теореме косинусов получаем

Следовательно, , и искомая площадь сечения равна

Так как центр вписанной в пирамиду сферы лежит на её высоте , то образует равные углы с плоскостями . Кроме того, из симметрии следует, что .

Проведём плоскость через перпендикулярно . Пусть эта плоскость пересекает в точке . Аналогично построим точки . Заметим, что треугольники равны, так как они прямоугольные, имеют общий катет , а углы равны, как углы между и плоскостями . Тогда и эти отрезки являются высотами боковых граней пирамиды. Из прямоугольного треугольника находим его высоту .

Рассмотрим треугольник . Пусть . Тогда по теореме косинусов

(1)

Так как и то

Полагая получаем уравнение

Откуда

Тогда из получаем . Так как , то является серединой а из равенства следует, что является высотой треугольника причём .

Пусть — радиус вписанной окружности треугольника .

Тогда . Из равенства

Тогда

Рассмотрим треугольник . Отразив точку симметрично получим точку . Пусть радиус сферы равен . Заметим, что он равен радиусу окружности, вписанной в треугольник . Тогда

Плоскость пересечет грань куба по прямой где ребро — в некоторой точке Пусть — середина и основания перпендикуляров, опущенных соответственно из точек и на плоскость Тогда так как и

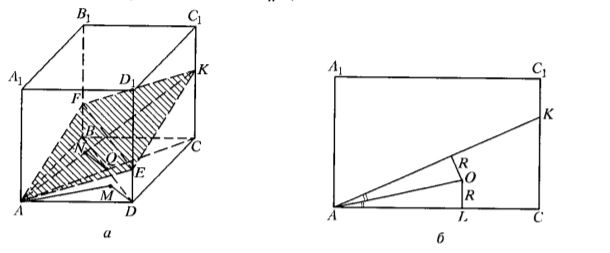
По условию откуда находим Из треугольника в котором находим и поэтому

Пусть — площадь сечения куба плоскостью тогда где и поэтому

Теперь найдём радиус вписанного шара. Заметим, что центр шара лежит на биссектрисе угла , а проекция точки на грань принадлежат Из треугольника в котором находим

где

Так как

тo

_____________________________________________________________________________________

Замечание.

Искомый радиус можно было также найти, заметив что он равен радиусу шара, вписанного в треугольную пирамиду где — точка пересечения прямых и точка пересечения прямых и используя формулу где — объем пирамиды — её полная поверхность.