Планиметрия на Высшей пробе
Ошибка.
Попробуйте повторить позже
Дан шестиугольник в котором
Докажите, что
Источники:
Подсказка 1
Вспомним условие на сумму углов в n-угольнике. Чем нам это может помочь? Для каких углов получается выразить величины?
Подсказка 2
Обратим внимание на четырёхугольник, образованный точками A, B, D, E. Какие свойства есть у вписанного четырёхугольника? Что ещё можно сказать про этот четырёхугольник?
Подсказка 3
Попробуем применить симметрию относительно середины отрезков BD и AE – какие новые точки и фигуры при этом получаются?
Подсказка 4
Рассмотрим полученные после отражения точки и параллелограммы. Какие стороны оказываются параллельны, а какие равны по длине? Можно ли использовать равенство углов и расстояний до прямой, чтобы сделать вывод о равенстве боковых сторон и параллельности оснований новой фигуры?
Подсказка 5
Вспомним, что средняя линия трапеции меньше её диагонали. Как это поможет доказать, что равенство возможно только в вырожденном случае?
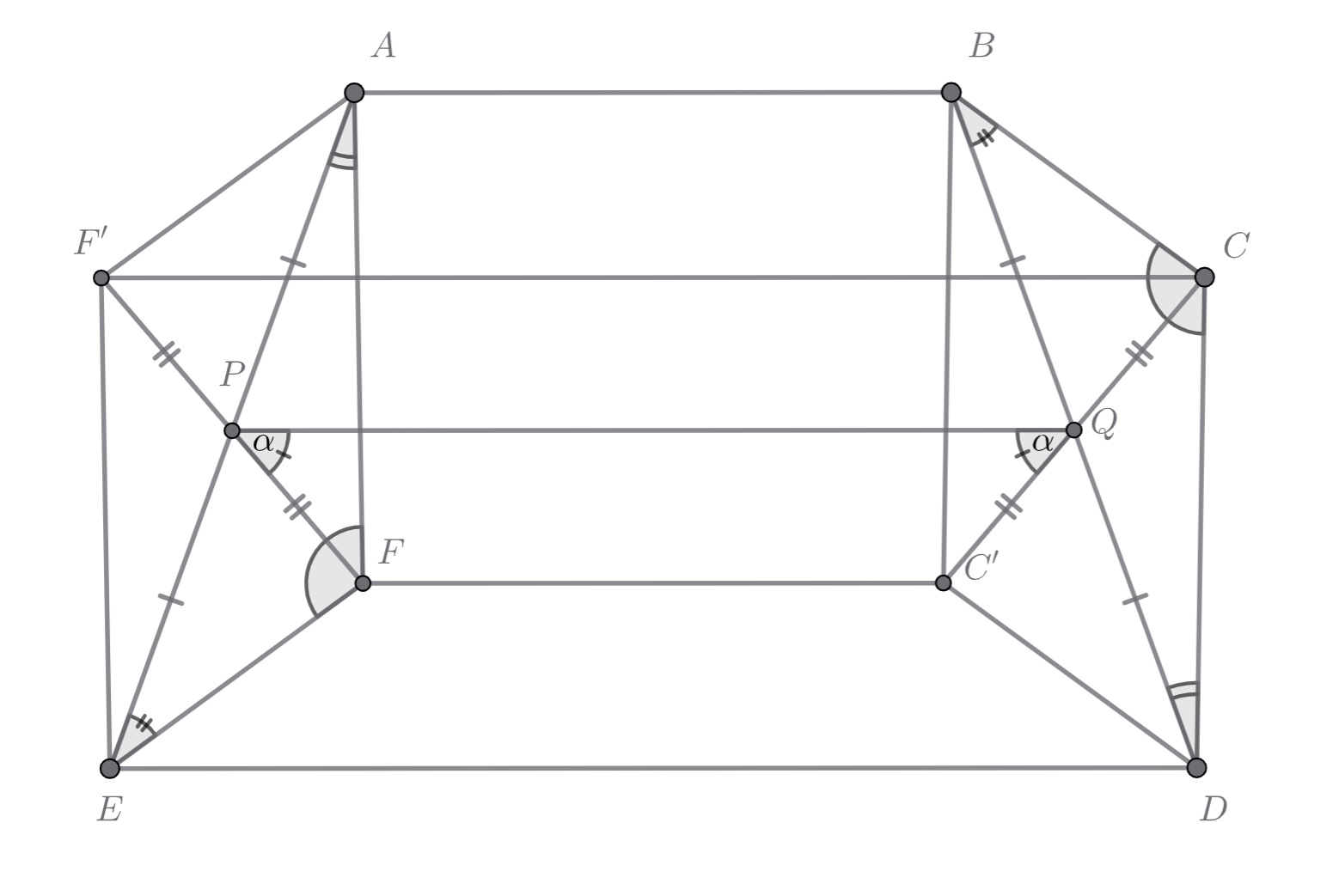
Так как сумма любого -угольника равна
то сумма углов любого шестиугольника, не обязательно выпуклого, равна
Поэтому из условия
следует, что
что, в свою очередь, влечет равенство треугольников
и
по двум сторонам и углу между ними. Так как углы
и
равны, а
четырехугольник
— вписанный. Хорды
и
его описанной окружности равны, поэтому
является равнобокой
трапецией.
Пусть, без ограничения общности, Отразим точки
и
относительно середин
и
отрезков
и
соответственно, получим точки
и
Параллелограммы
и
равны, поэтому
Отсюда делаем вывод, что Расстояние от точки
до прямой
равно
что равно
расстоянию от точки
до прямой
На то же расстояние удалены точки
и
от прямой
поэтому четырехугольник
является равнобокой трапецией с основаниями
и
параллельными прямой
(и, соответственно,
и
).
Кроме того, отрезок
является общей средней линией для трапеций
и
и его длина равна
Но в
отрезок
является диагональю, которая всегда длиннее, чем средняя линия, если трапеция невырождена.
Равенство
возможно только если
и
обе попали на прямую
и
является вырожденной
трапецией.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




