Планиметрия на Высшей пробе
Ошибка.
Попробуйте повторить позже
В окружность 
вписан треугольник 
такой, что 
Биссектриса внешнего угла 
пересекает 
в точке 
Прямая, параллельная 
пересекает стороны 
и продолжение стороны 
за точку 
в точках 
и
соответственно. Прямая 
вторично пересекает 
в точке 
Докажите, что точки 
лежат на одной
окружности.
Источники:
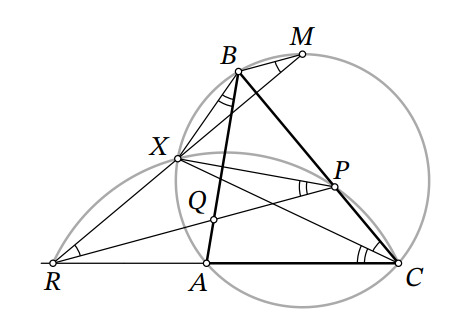
Докажем, что точки 
лежат на одной окружности 
т.е. что четырёхугольник 
является вписанным. Действительно,
как накрест лежащие при параллельных прямых 
и 
и секущей 
а 
как
опирающиеся на одну дугу в 
значит, 
Следовательно, по признаку четырёхугольник 
является
вписанным.
Из этого получаем, что 
Из окружности 
получаем, что
Значит, 
а, следовательно, по признаку четырёхугольник 
является вписанным, т.е. точки
лежат на одной окружности.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
