Планиметрия на Высшей пробе
Ошибка.
Попробуйте повторить позже
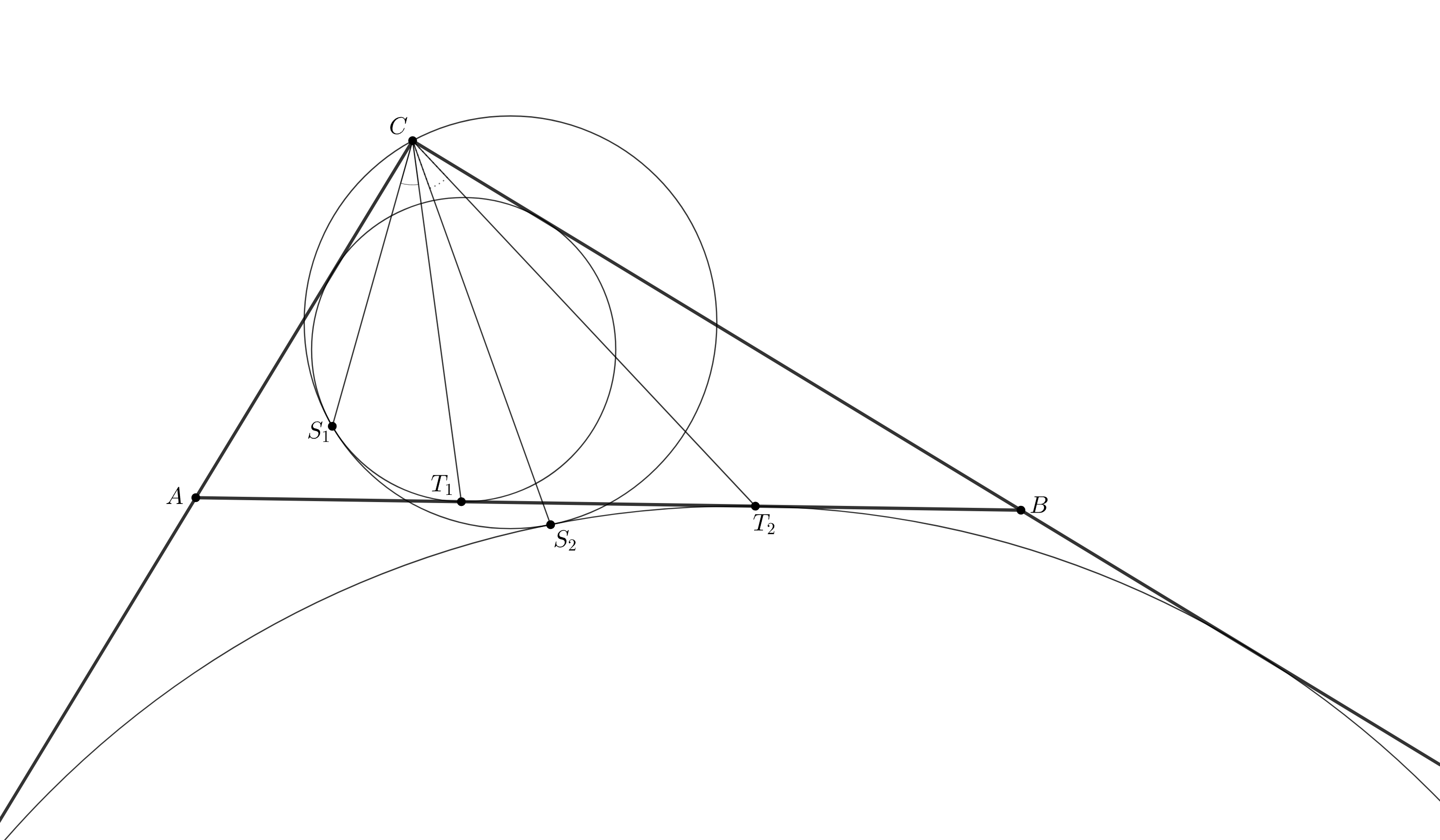
Гипотенуза прямоугольного треугольника
касается вписанной и соответствующей вневписанной окружностей в точках
соответственно. Окружность, проходящая через середины сторон, касается этих же окружностей в точках
соответственно.
Докажите, что
Источники:
Подсказка 1
Понятно, что скорее всего стандартный счёт углов тут не поможет. Здесь у нас и окружность Эйлера, и вписанная, и вневписанная. Так что либо нужны большие знания геометрических конструкций, либо какие-то хитрости. Пойдём хитрым путём. У нас есть как минимум три окружности на картинке, причём какие-то касающиеся. Какое преобразование плоскости тогда напрашивается сделать?
Подсказка 2
Верно, давайте сделаем инверсию с центром в точке C, причём сделать её с произвольным радиусом не слишком удобно. Давайте сделаем инверсию с радиусом √(ab/2), где переменные это стандартное обозначение сторон. Но если вы начнёте рисовать новую картинку, выйдет что-то не слишком хорошее. Какое ещё преобразование плоскости хорошо будет применить?
Подсказка 3
Смотрите, а давайте после инверсии сделаем ещё симметрию. Вот теперь осталось только понять, что и куда переходит после преобразований окончательно и почему мы выбрали такой радиус инверсии(на самом деле можно было без него, но так удобнее). В конце концов мы поймём, что углы переходят в друг друга, и победа!
Введём обозначения для длин сторон:
Сделаем инверсию с центром и радиусом
с симметрией относительно биссектрисы угла
Середины сторон прямоугольного треугольника и вершина его прямого угла образуют прямоугольник, значит, все четыре на одной
окружности. Значит, при инверсии образ окружности — прямая. Легко посчитать, что эта прямая отсекает от лучей и
отрезки
длины
и
соответственно, то есть симметрична
относительно биссектрисы угла
Поэтому гипотенуза и окружность Эйлера
треугольника переходят друг в друга.
Касательная из к вписанной окружности равна её радиусу
а касательная из
к вневписанной окружности равна полупериметру
Таким образом, их произведение
— площади треугольника
Итак,
Поэтому вписанная и вневписанная
окружности треугольника
переходят друг в друга.
Следовательно, переходит в
а
переходит в
Угол
переходит в угол
значит, они
равны.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




