Планиметрия на ММО
Ошибка.
Попробуйте повторить позже
Точка — середина стороны
треугольника
Окружность
проходит через точку
касается прямой
в точке
и
пересекает сторону
в точке
а сторону
— в точке
Пусть
и
— середины отрезков
и
соответственно.
Докажите, что окружность, описанная около треугольника
касается
Источники:
Подсказка 1
У нас есть с вами сразу три середины каких-то отрезков. Понятно, что можно тогда где-то найти средние линии и параллельности) Что из этого получится?
Подсказка 2
Из этого можем получить, что ∠XMY = ∠A. Теперь подумайте: что значит, что окружности будут касаться? Скорее всего, вы понимаете даже, где. Какое условие там будет выполнено?
Подсказка 3
Хочется, чтобы они касались в точке M, то есть нужно, чтобы описанная около XMY окружность касалась BC в точке M. То есть, ∠YMC = ∠YXM. А мы знаем, что ∠YMC = ∠ABC. По факту что нам достаточно теперь доказать?
Подсказка 4
Из знания уже одного угла нам достаточно доказать, что XMY подобен треугольнику ABC! Для этого попробуйте использовать то, что это средние линии, а нужные удвоенные отрезки можно выразить с помощью теорем о касательной и секущей :)
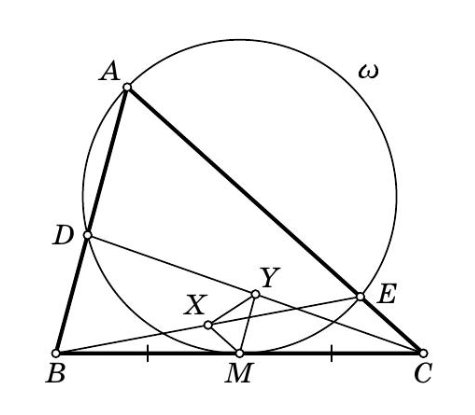
Заметим, что и
— средние линии треугольников
и
поэтому
и
Тогда
По свойству касательной и секущей к окружности имеем откуда
Аналогично получаем
Деля одно на другое и пользуясь тем, что находим
Получаем, что треугольники и
подобны по углу и отношению прилежащих сторон.
Тогда Получается, что в описанной окружности треугольника
угол, опирающийся на хорду
равен углу между хордой
и прямой
Это значит, что прямая
касается окружности, описанной вокруг треугольника
Следовательно, рассматриваемые окружности касаются.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




