Планиметрия на ММО
Ошибка.
Попробуйте повторить позже
Дана трапеция 
с основаниями 
и 
Перпендикуляр, опущенный из точки 
на сторону 
проходит через середину
диагонали 
а перпендикуляр, опущенный из точки 
на сторону 
проходит через середину диагонали 
Докажите, что
трапеция равнобокая.
Источники:
По замечательному свойству трапеции точка пересечения продолжений боковых сторон 
точка пересечения диагоналей 
и середина
основания 
точка 
лежат на одной прямой. Пусть 
— середины диагоналей 
и 
Тогда 
т. е. 
— тоже
трапеция, и по её замечательному свойству точка 
точка пересечения её диагоналей 
и точка 
лежат на одной прямой.
Следовательно, точки 
и 
лежат на одной прямой.
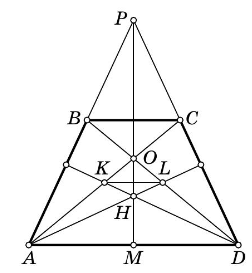
Для завершения доказательства рассмотрим треугольник 
в нём точка 
— точка пересечения высот к сторонам 
и 
следовательно, медиана 
проходит через его ортоцентр и является высотой. Таким образом, треугольник 
— равнобедренный,
откуда немедленно следует, что и трапеция 
— равнобокая.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
