Планиметрия на ММО

Первое решение.

Воспользуемся теоремой о прямой Штейнера: точки, симметричные произвольной точке описанной окружности треугольника относительно его сторон, лежат на одной прямой, проходящей через ортоцентр (точку пересечения высот) треугольника

Несложно заметить, что точка лежит на окружности, проходящей через середины сторон треугольника (это окружность девяти точек треугольника ).

По условию точка симметрична точке относительно средней линии, параллельной стороне Заметим, что точка симметрична точке относительно средней линии, параллельной стороне Получается, что прямая — это прямая Штейнера точки относительно серединного треугольника (треугольника, образованного серединами сторон треугольника ). Тогда на этой прямой лежит ортоцентр серединного треугольника, который и является центром описанной окружности треугольника

______________________________________________________________________________________________________________________________________________________

Второе решение.

Отметим середины и сторон и соответственно. Заметим, что треугольник — прямоугольный, а точка — середина его гипотенузы Значит, Поскольку точки и симметричны относительно прямой то Следовательно, точки лежат на одной окружности с центром в точке Отсюда так как эти углы опираются на одну дугу

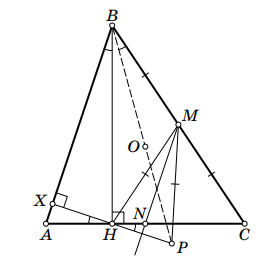
Обозначим точку пересечения прямых и через Заметим, что из-за симметрии точек и относительно прямой Кроме того, как средняя линия треугольника Таким образом, Отсюда следует, что

С другой стороны, заметим, что если точка — центр описанной окружности треугольника то как центральный угол, и из суммы углов равнобедренного треугольника получаем, что . Имеем а значит, точки и действительно лежат на одной прямой.