Планиметрия на ММО
Ошибка.
Попробуйте повторить позже
На стороне треугольника
взяли такую точку
что угол
равен углу
Чему равно наименьшее возможное
расстояние между центрами окружностей, описанных около треугольников
и
если
Источники:
Подсказка 1
Сперва введем все необходимые обозначения. Пусть O₁ и О₂ — центры окружностей, описанных около треугольников ABC и ABD соответственно. Тогда хочется найти минимальное возможное значение |O₁О₂|. Давайте отметим равные из условия углы. Что теперь очень хорошее можно заметить?
Подсказка 2
Правильно! Треугольники ABC и BDC подобны по двум углам! Давайте внимательно посмотрим на описанную окружность треугольника ABD и равные уголочки. На какую знакомую теорему это все намекает?
Подсказка 3
Конечно! Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними! Значит BC — касательная к окружности, описанной около △ABD. Что теперь можно сказать про О₂B? Вспомните, где расположен центр описанной окружности треугольника, и попробуйте оценить |O₁О₂|.
Подсказка 4
О₂B⊥BC. O₁ лежит на серединном перпендикуляре к BC. Пусть M — середина стороны BC. Тогда BM — ортогональная проекция O₁О₂ на сторону BC! Как связаны модули отрезка и его проекции?
Подсказка 5
Да! Проекция не длиннее отрезка, значит |O₁О₂| ≥ 1/2. Осталось лишь понять и объяснить случай равенства!
Пусть и
— центры окружностей, описанных около треугольников
и
соответственно, а
— середина стороны
Треугольники
и
подобны, так как у них угол
общий, а два других угла равны по условию. Поэтому оставшиеся углы этих
треугольников
и
также равны. Это означает, что описанная окружность треугольника
касается прямой
а радиус
перпендикулярен касательной
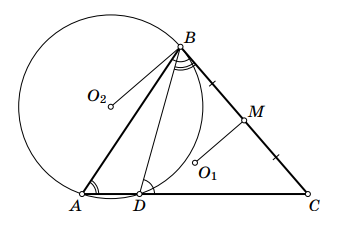
Кроме того, лежит на серединном перпендикуляре к стороне
Поэтому отрезок
длины
является ортогональной проекцией
отрезка
на прямую
Но проекция не длиннее отрезка, поэтому
причём равенство достигается, когда угол
равен
так как в этом случае
— середина стороны
а
— середина стороны
— средняя линия треугольника
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




