Планиметрия на ММО
Ошибка.
Попробуйте повторить позже
Точка — центр описанной окружности треугольника
Серединный перпендикуляр к
пересекает
и
в точках
и
Прямая
пересекает прямую
в точке
— середина
Описанная окружность треугольника
пересекает
описанную окружность треугольника
в точке
отличной от
Докажите, что прямая
касается описанной окружности
треугольника
Источники:
Подсказка 1
Нарисуйте большой чертёж циркулем и линейкой!!! Это ползадачи.
Подсказка 2
Несложным счётом углов докажите, что OA касается окружности AXY.
Подсказка 3
Пусть EM пересекает окружность ABC в точке F. Воспользуйтесь равенством углов ∠AEF и ∠AEM, поперебрасывайте углы и докажите, что направления на F и на O из точки A изогонально сопряжены относительно ∠BAC, отсюда будет следовать, что AF — направление на ортоцентр треугольника ABC, а значит AF ⊥ BC.
Подсказка 4
Используя параллельность MY и AF и вписанные углы (особенно, опирающиеся на дугу CF), докажите, что E,Y,M,C лежат на одной окружности.
Подсказка 5
Пользуясь доказанной вписанностью, докажите, что E лежит на описанной окружности треугольника AXY.
Подсказка 6
Ну а теперь воспользуйтесь тем, что OA = OE = R окружности ABC и поймите, что задача убита. Успехов!
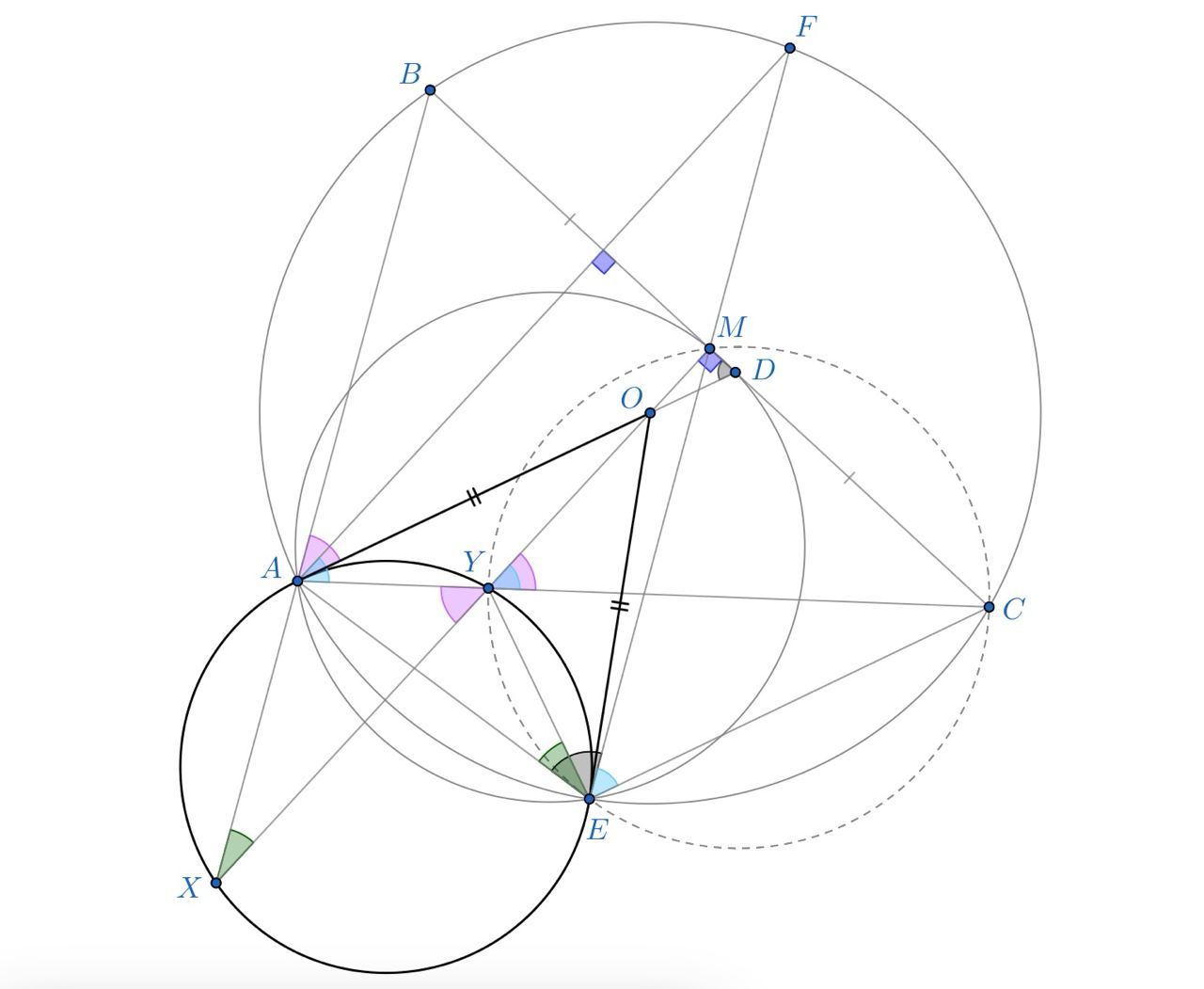
Заметим, что касается описанной окружности треугольника
так как
Пусть — точка на окружности, описанной около
такая что
Ясно, что
Получаем, что и
лежат на одной прямой. Кроме того,
что значит, что
и
лежат на одной окружности. Далее,
т. е. лежит на описанной окружности треугольника
Тогда
— касательная, так как
и
— касательная к
окружности
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




