Планиметрия на ММО
Ошибка.
Попробуйте повторить позже
Дан выпуклый четырёхугольник 
с попарно непараллельными сторонами. На стороне 
выбирается произвольная точка 
отличная от 
и 
Описанные окружности треугольников 
и 
вторично пересекаются в точке 
Докажите, что прямая
проходит через фиксированную точку, не зависящую от выбора точки 
Источники:
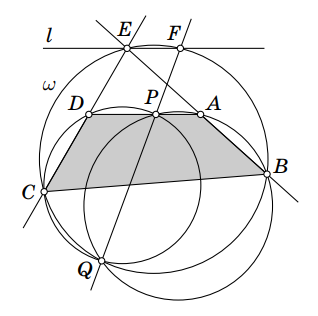
Обозначим через 
пересечение прямых 
и 
Рассмотрим случай, в котором точка 
лежит на луче 
за точкой 
Четырехугольники 
и 
— вписанные, значит, 
а 
Сумма углов треугольника 
равна
Следовательно, четырехугольник 
вписан в окружность 
— описанную окружность треугольника 
Обозначим через 
вторую точку пересечения прямой 
с 
Четырехугольник 
— вписанный. Значит,
Отсюда следует, что прямые 
и 
параллельны.
Пусть 
— прямая, проходящая через точку 
параллельно 
Тогда прямая 
независимо от выбора точки 
проходит через
вторую точку пересечения окружности 
и прямой 
Случай, когда точка 
лежит с другой стороны, разбирается
аналогично.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
